Math Made Easy: Word Problems in Seven Steps

The way most people react to them, one would think word problems are the bane of all existence. The fact of the matter is, almost all math problems worth doing are word problems. They are real-world situations, and in our attempts to grasp and communicate them, we must phrase them as words. How, then, do we dispel this aversion to them? How do we find an approach by which to break down that barrier which most people erect between themselves and a word problem the moment they see it? We do so by breaking down the problem itself, and adopt a systematic approach by which it effectively solves itself. I find the best approach to be in seven steps.

1) Write down all known information (in science, we like to call this your knowns), as well as the stuff you don’t know that needs discovering (your unknowns). Search through the problem, look for any quantities you know, and then write them down. Are there any distances involved? Masses/weights? Speeds? Perhaps just the number of items. Whatever they are, if you can identify something in the problem that is quantified, write it down. Likewise, go through the problem, and particularly the question, and look for any missing quantities – values you’d like to know, or that the problem demands, but are not given. Write down those as well.

2) Diagram the situation. Draw pictures representing just what’s going on, and label them appropriately with the quantities you identified in Step 1. If you need to draw more than one picture, such as before and after diagrams in the case of a problem involving two colliding objects, do so. It doesn’t hurt to have more than you need, and your pictures will help you see just what is really going on, and just what roles your identified values play in the story.

3) Note any formulae and expressions that are relevant to your situation and jot them down. Look at your knowns and unknowns – do you know of any mathematical formula that involves those type of quantities? For instance, if you have a speed, and a distance, and need a time, you might write: d=s·t (distance equals speed multiplied by time). Does the question make you think of any particular expressions? Write them all down. Again, it doesn’t hurt to have too many. You can always discard the ones you don’t need later, and having more than you need might actually help you pick the correct equation – perhaps the first one you thought of isn’t the right one, but seeing alternatives can help you realize that.

4) Review all the formulae you wrote, pick which ones seem the most relevant, and rework them into useful forms. This is just algebra. Frequently, you’ll find oyu have expressions that involve all the variables you wrote in Step 1, but aren’t written in a way that solves for the correct one. Take a look at my expression in the last step. It had all the variables we needed, but it solved for the wrong one – we knew the distance, but wanted to solve for time. No problem, we rework it, through algebra, to find t=d/s (time equals distance divided by speed). Now it’s in the form that is useful. We do this before we plug in numbers because it is much easier, and less writing, to do our algebra in variables rather than numbers (although some of our formulae may have numbers in them to start, and we keep them in to do our algebra correctly, such as the formula for kinetic energy KE=1/2·m·v²). Sometimes you won’t be able to find any one formula that has everything you need, and for which you have all the variables – that is, amongst the information you wrote down in Step 1 – except that one for which you are seeking an answer. That’s okay. That’s why we wrote down all the relevant expressions in Step 3. Look at them. Do you have parts of some in other formulae? Maybe you can substitute, plug one into another. And if you have more than one thing for which you’re seeking an answer, you’ll need at least one equation for each unknown piece of information.

5) Convert your units as needed for consistency. If you have one known in minutes, another in seconds, convert one of them so that they are in the same type of units. Check all your knowns, and make sure your units are consistent before moving on. Everything should be in either metric or imperial, not some in one, and some in another. Everything should be in the same scale – seconds or minutes, meter or kilometers, gram or kilograms, etc.

6. Plug your known numbers, including their units, into your reworked expressions. I think this step is fairly self-explanatory.

7. Solve! Once you have everything plugged into your reworked formulae, solving is easy! It’s now just a matter of adding, subtracting, multiplying and dividing (and in the case of more advanced problems, maybe some integration and derivation).

Let’s do an example:

You’re in a car, travelling at 50 miles per hour, approaching a train that is travelling 50 kilometers per hour. The train is one kilometer long. After you catch up with the rear of the train, how much further will you have to travel to pass the entire train? This problem is going to require a couple steps to solve, and that might not be obvious at first. So lets apply the method I’ve just laid out to help us break it down.

Step 1, write our knowns and unknowns:

I’m going to write them as variables to make is shorter, I’ll assign speed of the car s_c, the speed of the train s_t, the length of the train l_t, time to pass the train t, and the total distance travelled, d.

s_c=50mph

s_t=50kmh

t_l=1km

d=?

t=?

Step 2, diagram the situation:

Try to make your picture as close to scale as possible, but it’s not always necessary to be 100% accurate on your scale, as long as you label it correctly, and you’re able to correctly visualize the situation using your drawing.

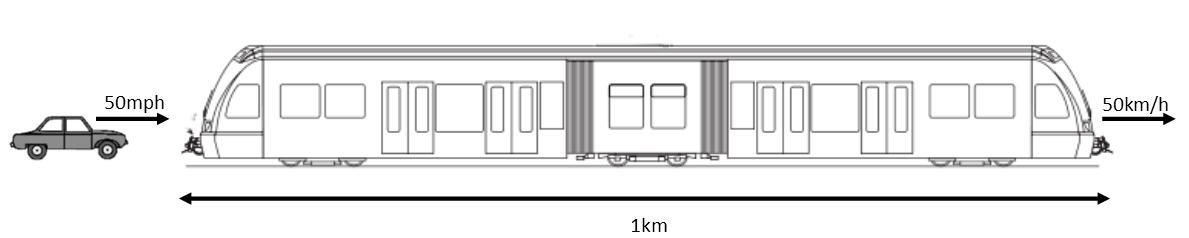
Step 3, write down all the relevant formulae I know. I see a distance formula in there, from the s, the d, and the t, so I write that down:

d=s·t

I also note that the speeds for the two vehicles are not relative to each other, but to the ground. In order to figure out how long it takes the car to pass the trains, I need the car’s speed RELATIVE to the train, so I’ll jot down an expression for that (and give it the variable scrt):

s_crt=s_c-s_t

After looking at the problem again, I think those are all I need.

Step 4) Review my formulae, and rework them as needed. I’ve only got one, but is it in the form I need? Well, it appears to be for the final question. BUT, I’m missing information I need for it. To find out how far the car travels in total while passing the train, I first need to find out how long it took to pass the train. To do that, I’ll need to rework the formula, as I did for my previous example.

d=s·t → d/s=(s·t)/s → t=d/s

Now I have my distance equation in two forms – one solving for distance, the other for time. I think I have what I need, so I’ll move on to step 5.

Step 5) I see that my units are not consistent. I have miles per hour and kilometers per hour. I also have a distance in kilometers. Since I have two units in metric, and one in imperial, I’ll convert that nasty imperial one to metric (plus, metric’s just easier to work with anyway).

50mph·8kmh/5mph=80kmh

Step 6) Now I can plug in my numbers. Let’s start at the equation for relative speed of the car:

80kmh-50kmh=c_srt

Now the time it takes the car to pass the train:

t=1km/c_srt

And the final equation:

d=80kmh·t

Step 7) Solve! I solve the first one, plug its answer into the spot for it in the second, and then that answer into the final equation:

80kmh-50kmh=30kmh

1km/30kmh=1/30 hr (or about 2 minutes since there are 60 minutes in an hour, but I’m going to leave this in fractional form)

80kmh·1/30 hr=2.7km

And we’ve solved our problem. The car travelled 2.7km along the ground in the time it took it to pass the length of the train.