Math Made Easy: Factoring

Of the many useful tools in our mathematical toolbox, factoring is one we will frequently use, sometimes without even thinking much about it. But there are times we need to use it, or when it can make our lives easier, but one might balk at doing so for sheer fear of being overwhelmed. Like most math, it shouldn’t be that way.

Let’s start by examining just what is factoring, and when should we use it? It’s fairly easy to define: it is the process by which we determine which numbers multiplied by another give you a certain starting number, the one being factored. Or, in other words, by which numbers is that first number divisible? But when is it useful? Well, besides when we need to determine how many things go into another (how many pairs of socks can I get for this much money?), we can use it to make problems with fractions, percents, and proportions easier, as well as those involving roots (like if we know the area of a house and need to figure out possible wall configurations). As I am fond of saying, and will address in another article, fractions make our life easier (not harder), and factoring makes them even simpler – and any tool that makes things easier to accomplish is certainly one we should master.

There are three main methods by which to factor, and the first one (and unfortunately one of the most commonly used) is absolute garbage. That one is the list method, where you try to write down all factors of (numbers that go into) a given number, usually in order. I say it’s garbage because it tends to cause the user to miss factors, even when they’re careful. I won’t waste anyone’s time by further discussing or illustrating this method.

The next method is the tree method. It’s mostly only useful when trying to simplify roots, which it does brilliantly, but when you need to identify all factors, it is also a poor method, as it will also miss some due its nature of pulling out some factors more than once. In this method, we start by writing the number we want to factor, taking care to give ourselves room to create a branching tree beneath it, of which it is the peak. We then draw two branches below that number. At the end of the left one (by convention), we write the smallest number (other than one) that divides evenly (meaning with no remainder) into the original number. At the end of the right branch, we write whatever number by which we must multiply the left-hand number to get the top number. For instance, if we wanted to factor 14, the branch to the left would have a 2, and on the right, a 7, since 2x7=14.

We then examine the right-hand number to see if we can find anything that goes into it – if we don’t, we’re done. If we do, we repeat the process with the right-hand number being our new starting number. In my previous example for 14, we would be done, because 7, being a prime number, is only divisible by 1 and itself. But if we were factoring, say, 20, our first left and right numbers would have been 2 and 10, respectively (since 2x10=20). We would then look at the 10, realize 2 also goes into it, draw our new branchs from the 10, and write a 2 on the left and a 5 on the right (since 2x5=10).

We repeat this process as many times as we need until we can no longer find any numbers that go into the bottom right number. Here’s a more involved example:

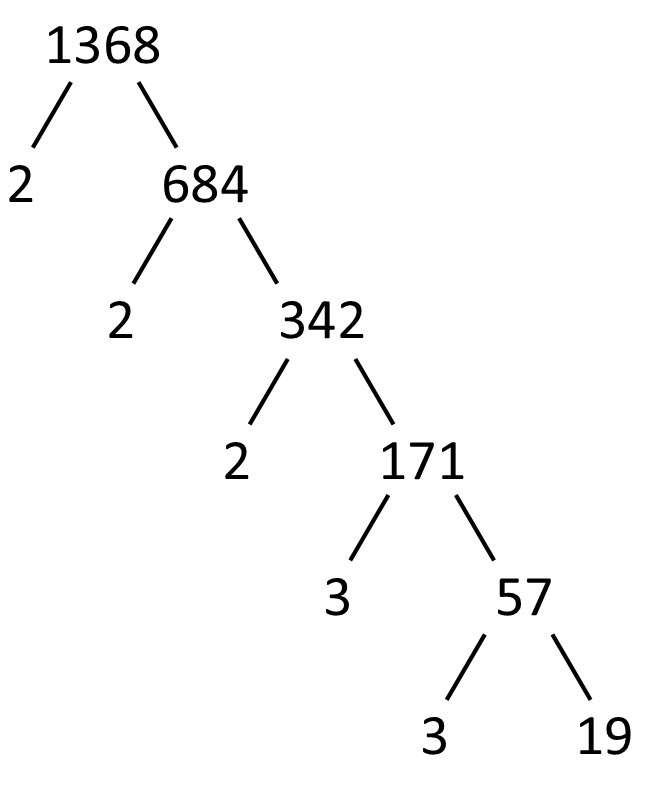
Remember I said we really only want to use this method when we’re simplifying roots, and I mean it. It’s useful for that, incredibly so, as all we care about for root simplification are the left-hand and bottom-right numbers in the factor tree. What we do with those, I’ll save for another article. But the reason we don’t use it for anything else is we actually can miss quite a few factors, as I’ll demonostrate using my preferred method.

My main method for factoring is what I call the pairing method, and it is absolutely the best method to use if you need to find all factors of a number. Use it properly, and you will not miss any of them. Further, the method has the advantage of informing you when you’re done, so you don’t have to guess about that.

Start by writing down the number you wish to factor, write a dash, and then the number one. This is your starting pair, and indicates that you recognize that the number is divisible by 1 and itself, as are all numbers. Then consider the number 2. Is your starting number divisible by it? If so, write it down under the 1, a dash, and under the starting number whatever the result of it divided by 2 is (or think of it as what times 2 equals the starting number). You don’t have to write down 2 unless it is a factor, but when you’re getting used to the method, it may be helpful to do so when you’re considering it – just make sure to cross it out if it’s not a factor. Then repeat this process, one at a time, for each number counting up (2, 3, 4, 5, 6, etc) until you’ve uncovered all the factors. The advantage of writing them down in pairs, and with a one-up count, is twofold: you won’t miss any, and you’ll know when you’re finished. But how do you know you’re done? Take a look at my factoring example below, for the number 1368:

Note how, as you add pairs, those pairs are coming closer and closer together – there are fewer possible numbers in between each one. Well, that very pattern is what tells you that you’re done – once the pairs have come together, and you’ve tested all possible numbers in between the last pair (usually not that many, like in our example where 37 is the only number left), you’re done. You’ve found all the factors. Now how many more factors of 1368 did we find in my example than we did using the tree method – 17 of them! The pair method is far more complete.

Now, beyond using the appropriate method (tree method for simplifying roots, pair method for everything else), how can we make factoring easier? Do we have to do long division to test every single number? If so, than to factor 1368, we would have had to do 36 long division problems. Forget that! Thankfully, we don’t have to do so. Many numbers have tests we can apply on the original number to tell us whether they are a factor of it. Here they are:

2 – All even numbers are divisible by 2

3 – Add all the digits of the number. If the result is divisible by three, the original number is also. If you’re not sure, add the digits of the results and see if that is divisible by 3. Example: For 1368, we add 1+3+6+8=18, which is disable by 3, so 1368 is (and 1+8=9, which is also divisible by 3, confirming 18 is).

4 – The test for four comes in two parts. The first thing to do, is look at the second to last digit of the number. Is it even, or odd? If that second to last digit is odd, then the number must end in a 2 or 6 for it to be divisible by 4. If the second to last digit is even, then the number must end in a 0, 4, or 8. In our example of 1368, we see the second to last digit is a 6, which is even, so it must have 0, 4, or 8 as the last digit. As the last digit is 8, we confirm it is indeed divisible by 4.

5 – The number must end in a 0 or 5 to be divisible by 5.

6 – If the number is divisible by both 2 and 3, it is also divisible by 6. So if you’ve written down both 2 and 3 in your factor pairs, you know 6 is also a factor. For our example of 1368, it is divisible by 6 since we found it to be factorable by both 2 and 3.

7 – I wish there were as test for the number 7, but there is not. It is the most ill-behaved of numbers (as we’ll see again in my article on fractions).

8 – While there is no hard and fast test for 8, we can at least make one to tell if it’s worth our time to do long division to see if it is a factor. If the number is divisible by both 2 and 4, it may also be divisible by 8, so go ahead and do the division to see. If you haven’t already written both 2 and 4, don’t waste your time. Now, the reason this is not a hard and fast test, and instead is a “is it worth your time test,” unlike with 6, is that, 4 is not a prime number. It is, itself, factorable by 2 (2x2=4). So if something is divisible by 4, it is ALWAYS going to be divisible by 2. So having both on your list doesn’t automatically mean that your original number is certainly divisible by 8, just possibly.

9 – The test for 9 is similar to the test for 3. Add all the digits, and if your result is divisible by 9, so is the original number. For our 1368 number, 1+3+6+8=18, which is divisible by 9, so 1368 is (and 1+8=9, confirming that 18 is).

10 – Only numbers ending in 0 are divisible by 10.

After 10, fewer numbers have tests you can do. These are limited to all numbers that have 2 or more prime numbers as their only factors. If you’ve written all those prime numbers in your pair list, then that number is also a factor. Example: If we’re factoring 360, we will have written down 3 and 5 when we went by them and tested them. 15 is divisible only by itself, 1, 3, and 5. Since we’ve already written 3 and 5, 360 must also be divisible by 15.