Math Made Easy: Fractions Are Your Friends

The very mention of the word “fractions” brings frowns and grimaces to the majority of people’s faces. They react as though fractions are a foul medicine to be avoided at all costs, only to be resorted to when all else fails. The truth of the matter is, fractions can, and should, be your friends. They will make your math, and thereby your life, much easier should you learn to master them, and learn all the tricks of manipulating them with ease. So let’s examine fractions, and see what those tricks are. How do they help us, and how do we make them easy?

So just what *is* a fraction in the first place? I’ll ask my students this question, and almost none of them can answer it. They’ve been forced to memorize methods, but never really had explained to them just what’s going on, or what they’re really doing. So, let’s try to understand what they are first.

There are a couple ways you can think of what a fraction is, and it’s best to remember them both, so that you can look at them from different angles depending on the situation – which ever makes that situation clearer. At their core, a fraction is an operation. Specifically, it is a division problem. It is telling you to divide the top number by the bottom number. We’ll remember this later to make our math easier. Further, they are ratios, proportions. They relate one thing to another, and give us a visual aid to their relative sizes. And while sometimes that may not be obvious at first, by making use of the fraction, and properties of the fraction, we can usually reduce it to something that makes the proportion more accessible, more readily seeable.

Now that we know what they are (both a division problem and a proportion), let’s look at how they make our math easier.

Most humans are not very good at division. Our brains just don’t work in that direction very well. We’re good a multiplying – most people by the time they’re adults have no problem multiplying 25 x 4, or 25 x 6, or even 32 x 3. But go in the other direction, and divide, and most people will hesitate before they answer, and the more complex the division problem, the longer they’ll hesitate. So answering, 100÷4, or 150÷6, or 96÷3 takes them longer to do. The best thing about fractions, is they allow us to take a division problem, and turn it into a multiplication problem. And in many cases, it’ll even allow us to solve the entire problem without doing any long division. How? By expressing it as a fraction, and then simplifying until I get my result. Often, that’s all I need to do – I’ll never need to actually do long division.

Remember that when you simplify, you seek common factors between your numerator (your top number) and your denominator (your bottom number) and “take them out” of both of them, reducing the size of both by the same amount in the process. I’m going to do an example and discuss steps to follow when doing your fractions:

The example: I’ve got $45.00 I want to buy a bunch of candy bars that are each $1.25. I want to know how many candy bars I should put in my basket. Well, I could do long division, but that’s going to be a pain in the butt.

Recognize that any division problem is just a fraction. Write it as such.

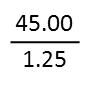
Get rid of any decimals. Normally in school, you’d be told to multiply the top and bottom by some multiple of 10 that’s big enough to account for the decimal places, effective removing them. It’s easier than that. Pick the number in your fraction that has the MOST decimal places. In my example, they both have the same number of decimal places (two), so it doesn’t matter. Move the decimal point to the right until you’ve moved it as far as you can, counting how many times you’ve moved it (here, again, twice). Now go to the other number, and move it to the right the same number of times, adding a zero each time if you go beyond the last digit of that number. In my example, I don’t have to add any zeros.

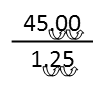
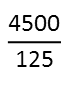
Simplify. Again, this just means finding any common factors between the two, and essentially getting rid of them so they both become smaller by the same amount. Check out my article on factoring for some tips on how to easily factor. Remember that when you pull out the factors, you’re dividing both the top and bottom by that same number. And when you simplify, you don’t *have* to go straight to the greatest common factor like you were taught in elementary school. That just takes too long. It’s okay to simplify in steps, doing so multiple times until you get to the simplest form of the fraction. And, usually doing so will actually be FASTER than trying to bang your head over what the greatest common factor between the two is so you can simplify in one step. Continue simplifying until you can’t any longer. You’ll end up with either a whole number, or a more comprehensible fraction. In my example, I immediately see they’re both divisible by 5, so that’s what I’ll simplify them by first.

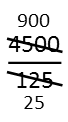
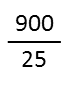
Again, I immediately see the resulting new numerator and denominator are still divisible by 5, so I do it again.

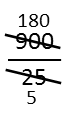
And again.

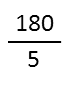
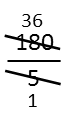
Now I’ve got something over one. Anything over, or divided, by 1 is itself. So I have my answer. For my $45.00, I can buy 36 $1.25 candy bars.

That’s it for handling a single fraction. Easy, no?

But fractions are more than just that. They can make much more complex math problems easier, as well. The key is twofold: always find a way to turn division into multiplication, and to simplify before you multiply. The former takes the difficult and makes it easier, and the latter eliminates most of your work – it’s hard to multiply big numbers, but it’s easy to multiply small ones, and simplification makes your numbers smaller. How do you turn division into multiplication? Just remember that fractions are division. Express your division problem as a fraction, and you’ll see you’re multiplying instead of dividing.

And as far as simplifying before you multiply – remember that as long as you are multiplying fractions, no matter how many there are, if they’re ALL being multiplied together, you can pick *any* number from up top and *any* number from the bottom for simplifying. But only one pair at a time – don’t try to pull one factor out of more than two numbers at once, or you’ve messed up.

The 10s trick – if you ever see zeros at the ends of your numbers in both top and bottom, you can just cross out an equal number of zeros on both the top and the bottom. This is effectively reducing the fraction by some multiple of ten.

The same number trick – if you see the same number in top and bottom – GET RID OF IT in both places (but only in pairs, one for one). It effectively becomes 1.

Here’s another example. A pair of $125 pants are marked as half off. But there’s a sale going on today that’s a 20% off everything sale. Sales tax is 8%. You want to know what you’ll have to pay at the register. This seems like it might be a complex problem, but it really isn’t. IF we use fractions! And percentages are just fractions – you just place that number over 100, and, voila, fraction. So let’s do this one. Remember that a tax is ADDING to something, so add that 8 to 100, then put it over 100 to do it right. And a discount is SUBTRACTING, so you need to subtract that from 100 before putting it over 100 for your fraction. (ie, the 20 percent discount here is 100-20=80, then put that 80 over 100).

First, we recognize that half off is dividing something by two. But I don’t want to divide – I want to multiply. Especially since $125 doesn’t divide by two evenly. So I’ll write that as a fraction. Then I’ll write each of those percentages as a fraction. Then I’ll set up a chain of multiplying. It’ll look like this (note I expressed $125 as a fraction by putting it over 1):

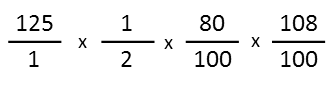
Right off, I see one fraction where I can cross out one zero from both the top and the bottom. I’ll do that.

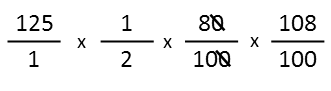
Now I see that both two and 8 are divisible by 2, so I’ll apply that step.

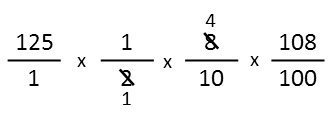
Next, I see 10 and 108 are both divisible by 2, so I’ll do that.

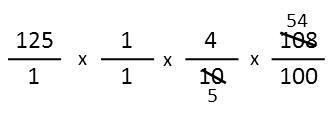
125 and 5 are both divisible by 5, so that’s my next step.

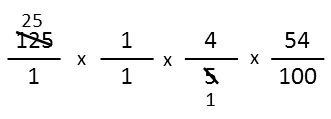
We all know there are four quarters in a dollar, and that a quarter is worth 25 cents. This means 100 is divisible by 25, exactly four times. So I’ll take care of that next.

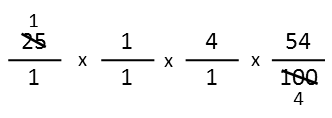
Then I see that 2 fours, one on top and bottom. I’ll get rid of both of those.

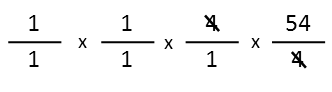
And, voila, I’m left with nothing but 1s and the number 54. That’s my answer. I’ll have to pay $54 exactly, including tax, at the register. But remember simplifying along the chain ONLY works with multiplying fractions, not with adding and subtracting.

Which leads me to the last topic about which I have to speak – adding and subtracting fractions. Sometimes we have to do this, and people will frequently look at the problem like it’s asking them to stab themselves. But it's really not all that hard. Just remember three things:

First, you can't add the bottoms. When adding and subtracting, the bottoms don't interact at all, only the tops.

The next thing to remember when adding and subtracting fractions, is you simply can’t do it unless they have the same denominator. You’ve got to make the bottoms match. And the way to do it, is to multiply them by the version of one you need to make them look the same. This might make you say “Huh? What’s that mean, I thought 1 was 1 and that’s it.” Well, just as I was able to express 125 as 125/1, you can express one in lots of different ways. Any number divided by itself is 1. That means any number over itself is 1. That means we can multiply fractions by 1, changing their appearance, but not their value. That allows us to give them a common denominator. Our job is just to figure out which version of one will work. And sometimes you have to multiply one by one version, and the other fraction by another. Such as adding 1/2 and 1/4. Here, I see if I multiply 2 by 2, I get four, so the version of one I need is to multiply 1/2 by 2/2. I don’t have to do anything to 1/4.

Finally, unlike in multiplication, do NOT simplify before you multiply. That'll just defeat the purpose of giving them common denominators, and you'll be right back where you started.

Example: Let’s talk pie. John and I bought pies from a shop that has them sliced in 12 slices. I have ¾ of a pie, John has 2/3 of a pie, and together we ate half a pie. How many slices of pie do we have? First, we need to add everything together. For simplicity’s sake, let’s do the addition and subtraction first:

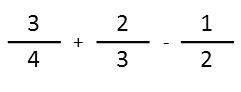
So, to figure out the lowest common denominator, I see that two can be multiplied by 2 to give me four, but that doesn’t help since three can’t. BUT, if I multiply 4 by 3, and 3 by 4, I get twelve. So I need to multiply my first fraction by 3/3, the second by 4/4, and the third by 6/6 (since 2x6=12). It looks like this:

And gives us:

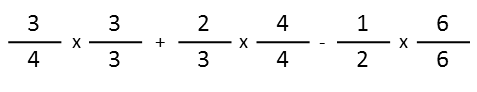
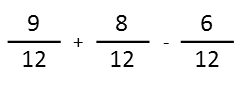
Now we can just add the top numbers, basically ignoring the denominators except to write it down. 9+8=17, and 17-6=11, so we get: Now the wonderful thing? Since our pies were divided into 12 slices, and we have 12 as a denominator, we know that we have 11 slices of pie left. That’s it! We’re done.

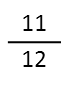
One last note: NEVER work with mixed numbers (a whole number and a fraction together). They’re horrid. We can’t do easy math with them. The only reason you ever really worked with them in elementary school was to give you a better feel for the value of fractions. It’s much better to do you math with improper fractions (a bad term) – in other words, it’s okay for the numerator (the top) to be bigger than the bottom (as we saw in my last example when I put 125 over 1). And the best way to convert a mixed number to a fraction is treat it like an addition problem, placing the whole number over one, giving the two a common denominator, then adding.

That’s it. Fractions really are that easy, and really do make your life a lot easier, if you remember the rules and tricks of manipulating them, which really aren’t all that hard. Remember to: simplify before you multiply, treat division as multiplication, simplify by the first thing that comes into your head, find a common denominator when adding or subtracting, and never work with mixed numbers. Remember those things, and they’ll never be a bother again.