Math Made Easy: Inverse, Reciprocal, and Opposite

One of the keys to being successful in mathematics is understanding the exact meanings of the nomenclature we use to describe it. Some terms, however, are almost universally misunderstood, or conflated with other words. Three commonly confused terms are opposite, reciprocal, and inverse. Many people these three words mean the same thing, or at least something very close to each other, which absolutely couldn’t be further from the truth. To understand this, where the confusion comes from, and how we can remember to distinguish the three, let’s examine them all more closely.

Inverse: Many dictionary, and textbook definitions of this word don’t help at all in figuring out exactly what it means in mathematics. Just what does “reversed in order, nature, or effect” mean in math? Here’s the best way to think of the inverse: it is what needs to be done to something to undo it. There are three ways we can do this, and hence the source of confusion – two of the ways are really just the reciprocal and the opposite, which I’ll discuss in their own sections. The third way, and the true inverse, is basically whatever you need to do to a function to return JUST one variable – usually the variable defined along the horizontal, or x-axis, when graphing the variable. Not all functions have an inverse function unless we restrict the function to a certain domain (range of values for the variable we’re discussing, in most cases, x). To find the inverse of a function, we select the axis along which we are seeking the inverse (again, usually the x-axis since most two-dimensional functions are already written to solve for y), solve for that variable, and then swap the variables. I’m not going to discuss more complex functions involving more than two variables, or matrices. Integers do not have an inverse in this respect – they can only have reciprocals or opposites. The physical appearance of an inverse can sometimes be quite surprising – I’ll be graphing the function x² and its inverse as an example below.

Reciprocal: Sometimes this is called the multiplicative inverse. The reciprocal of something is that element which, when multiplied by our original thing, gives us 1. For matrices, the reciprocal will return the identity matrix, and is usually called the inverse matrix, further leading to the confusion of these three words. For fractions, we just flip the fraction over. For integers and most functions, we treat them like a fraction (over one since everything is really just a fraction over one, since everything divided by one is itself), and then flip that fraction – in other words, put it in the integer or function in the denominator (bottom) of a fraction with one on top. For many functions, the reciprocal has the appearance of turning the function inside out. For others (like the tangent and its reciprocal the cotangent), it has an appearance very similar to the opposite of the function.

Opposite: Sometimes called the additive inverse, the opposite of a thing is what we need to add to that thing to cancel it out, or get zero. For integers, matrices, and virtually all functions, we just change the all the signs – negatives become positives, positives become negatives, subtraction operators become addition, and addition operators become subtraction. When finding something’s opposite, care must be given to address every sign correctly. Physically, something’s opposite is its reflection (as we’ll see in the graphs below).

Now let’s do an example. I’m going to do the relatively easy function y = x², to demonstrate how to take it’s inverse, reciprocal, and opposite, and demonstrate just how different they all are with its graphs.

When we graph y = x², it looks like this:

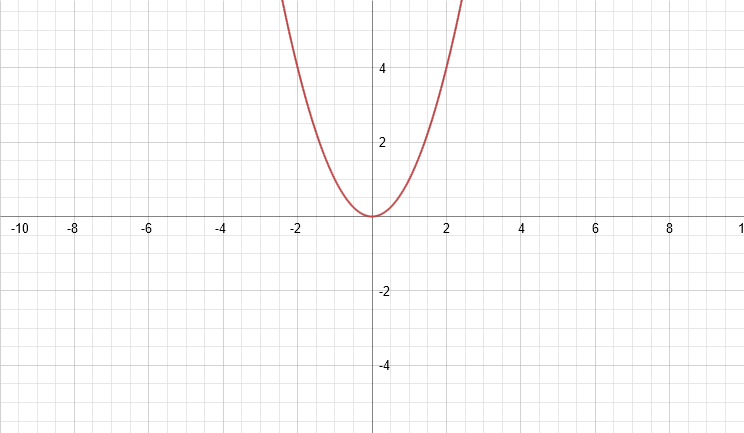
Let’s start with its inverse: since the function is already solved for y, we will find the inverse with respect to the x-axis. First, we solve for x:

y = x² → √y = x

Now, we swap the variables:

y = √x

Now we note that the inverse function CANNOT exist when x is negative - that'll put a negative number inside the root, returning an imaginary result. So we have to restruct the domain (the possible values of x) to x>0. Doing that, we’re done. We now have the inverse function. Note that if we insert it for x in the original function, the square exponent and the square root radical cancel each other out, giving us y = x, satisfying the definition of an inverse I gave above – the radical undid the square.

Graphed, this inverse function looks like this:

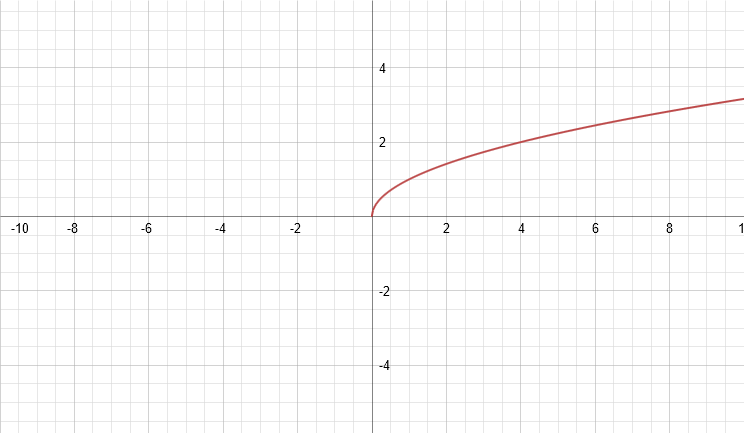
When we take the reciprocal of y = x², we just express it as a fraction over one, and then flip the fraction upside down:

y = x² → y = x²/1 → y = 1/x²

If we multiply our original function by this, we find we have x²/x², which is simply 1, meeting the definition of a reciprocal.

Graphed, y = 1/x² looks like this (note how it appears to turn the original function inside out):

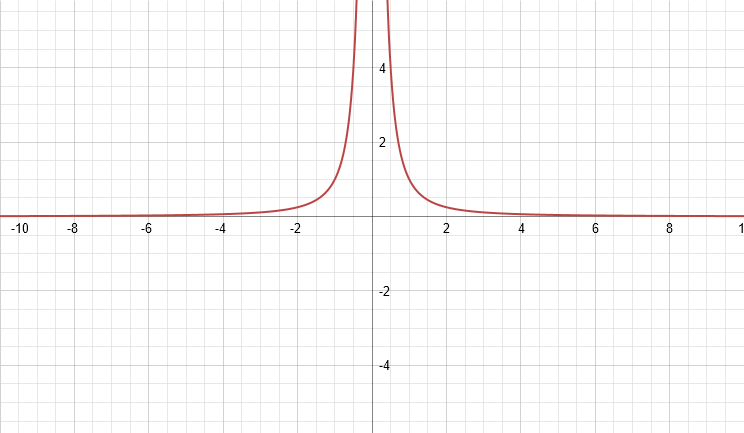
Finally, let’s take the opposite of the function. Since there’s only one term in it, we only have to worry about one sign.

y = x² → y = -x²

If we add x² and –x², they cancel out, giving us zero, meeting the definition of an opposite.

Graphed, -x² looks like this, just a reflection of the original function:

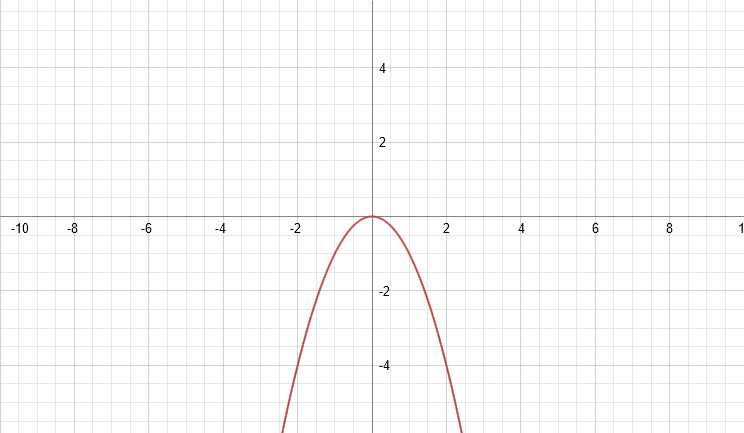
Now that we can see all three graphs, look just how radically different they all are. The results they produce are absolutely nothing alike, and clearly demonstrate just how important it is we do not confuse and mix up these terms.