Math Made Easy: Multiplication

One of the beauties of mathematics, is that there are often times multiple ways to complete an operation. It’s like a tool box, where we can pick and choose from various tools the best tool for the situation, with which we feel the most comfortable. And, as I am fond of saying, since math is a tool, we want it to work for us, and not the other way around. Let’s look at one of the four simple operations, multiplication.

As it turns out, I am known for being able to multiply large things in my head, frequently faster than people can punch the numbers into a calculator (or as fast, as the number gets bigger). For a while, I thought nothing of it, until my students kept asking me how I was doing it. So I gave it some thought, and I realize that the method I used in my head was not the traditional method you and I were taught in school, or that I used on paper, which led me to stand at the white board and try to transcribe what exactly was going on in there.

I found that it is actually a very simple system that eliminates a lot of the juggling one is required to do with the traditional multiplication method. In that method, one is required to carry numbers over and sometimes hold multiple rows of numbers in the ready for addition at the end of the problem. This requires that, if one is to attempt the operation mentally, one is sometimes jugglings upwards of 5-8 elements in their head at any given time. In my method, you are never juggling more than 4 elements at once, and you are never multiplying anything larger than single digit numbers, which vastly simplifies and expedites the process.

How does this work? First I will describe the process, then I will walk through an example. Note that I actually slightly modify the method in writing to make it faster there. So I’m going to describe it as I do it in writing, and will note where I do it differently in the mental technique.

First, I write down the numbers as I normally would in the traditional method.

Then, as I multiply, I start on the FAR LEFT ones first, rather than the far right ones as in the traditional method. If that sounds kooky, bear with me, it’ll soon make sense.

So, multiplying ONE digit at a time, starting on the far left, I first count all the digits to the right of the ones on which I’m currently working, and write down one zero for each of them. I then multiply those two left-most digits, and write down that result on the left of the zeroes. Then, staying on the far left one on the bottom, I move to the next one on the right in the top row, again counting everything to the right of those, writing down the zeroes as a new row, and then the result of multiplying those two digits. I repeat this until I’ve multiplied the far left number on the bottom by all the top numbers. Then I repeat the process for all the digits on the bottom, working my way from the far left, to the right. Once I have completed this, I simply add all the rows, and I am done. You’ll find the addition is quite simple and fast, as most of what you’re adding is just zeroes. (and here is the only difference between the writing version of this technique and the mental: since I am trying to cut down on how many things I’m storing in my head at once, I add the rows as I go, so I only have 4 things in my head at any one time: the 2 numbers I’m multiplying, and the two rows I’m adding).

Example:

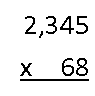
Starting with the 6 and the 2, I count all the numbers to the right, of the six and two, and find there are four of them (345 up top and 8 down below), so I write down 4 zeroes:

Then I multiply 2x6, which is twelve, and write that down to the left of the zeroes:

I have effectively multiply 2000X60, which is 120,000. I now repeat the process for 3x6, staying careful to line up my zeroes if

I’m writing, or to add the two rows at this point if I’m doing it in my head:

And so forth until I’ve multiplied 6 by the entire top row:

And now I repeat the process for the 8:

Once I have completed multiplying all the digits, I simply add my columns: Note I actually have no more than 4 digits to add in any column – it’s mostly just zeroes!

Now, this admittedly is a little bit more writing than the traditional method, but since most of what you’re writing is zeroes, it does work out to be a *lot* faster, as you’re not struggling with carrying, or worrying about losing your place when you’re doing large numbers, because the zeroes do it for you. It turns out, that the bigger the number, the simpler it is to multiply this way. And when you’re doing it in your head, since you add each row as you go, you never have more than 4 things in your head at once, and don’t have to worry about whether you carried that number correctly.

Give it some practice, and if it works for you, make use of it! You now have one more tool in your mathematical arsenal. Just remember you can always fall back on the traditional method if need be. Math is about what works for you, not you for it.