Math Made Easy: Transformations of Functions

I have previously discussed the characteristics of polynomials, and how all math is just a tool to describe the physical world. Given that, it should not be surprising that there are some basic things one can do to any function, that will change, or transform, that function in a consistent and predictable manner. In fact, there are four things that can be done to any function, each which will change that function in the same way, no matter what it is – be it an exponential, linear, trigonometric, differential, or integral function, these four things transform them all identically. To examine this, let us define a general form to talk about all functions. I’m going to use this:

y=afun(bx+c)+d

Where a, b, c, and d are the four things you can do to the function, fun is the function, and x is the input variable, y the output variable. As examples, I’ll use a linear function, and quadratic function, an exponential function, and a trigonometric function, so that we can see that these four things do indeed affect all four functions the same way. Note that we read this as: multiple x by b, add c, apply the function, then multiply that result by a, then add d. In other words, we work from inside the function to the outside. Let’s look at their basic graphs:

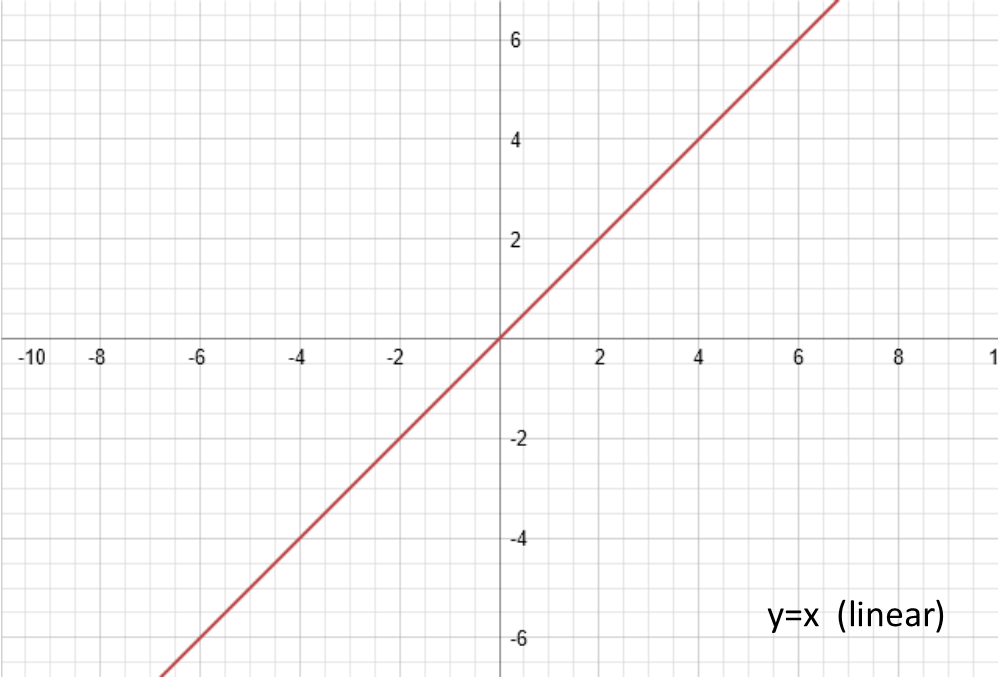
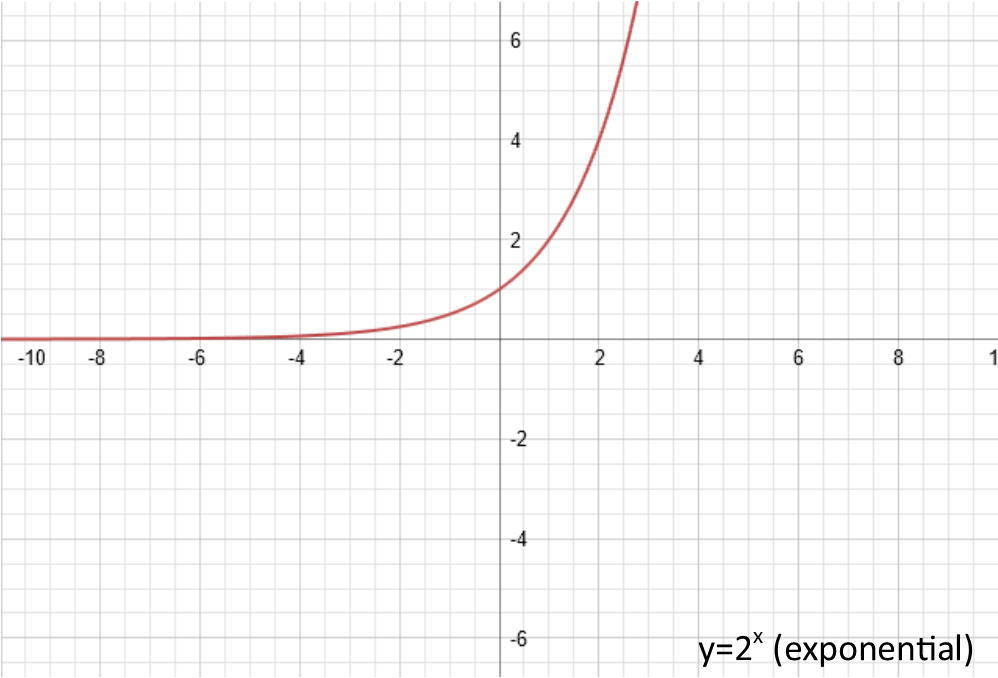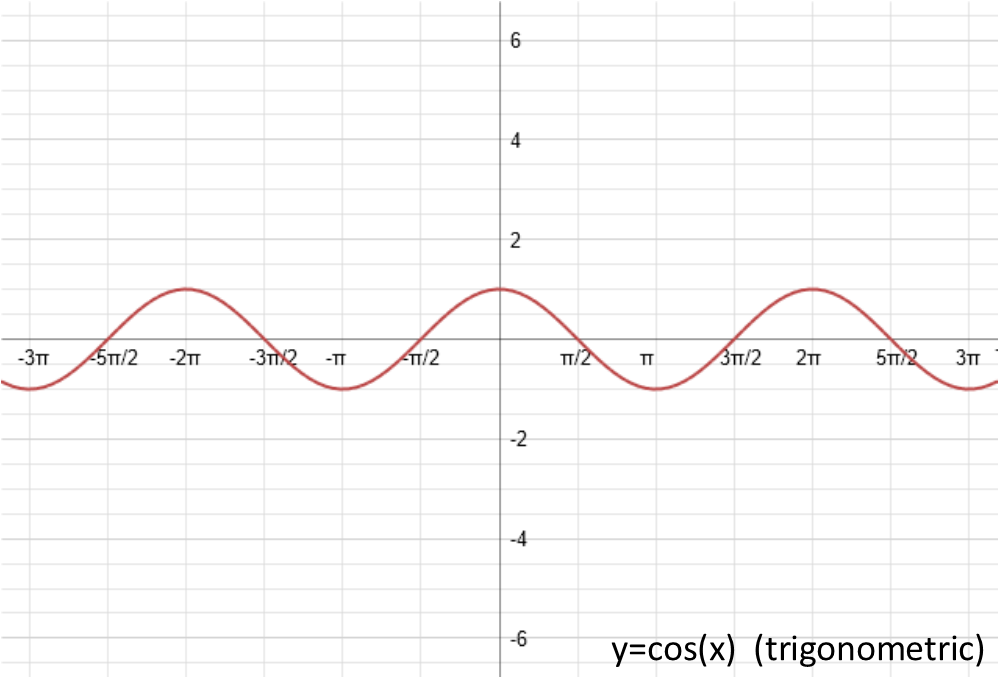
Now, I’m not going to address them in alphabetic order, but rather in the order of ease of understanding them. Which means I’m going to start with d – in the reverse order of how a, b, c, and d are applied when we actually do the computation.

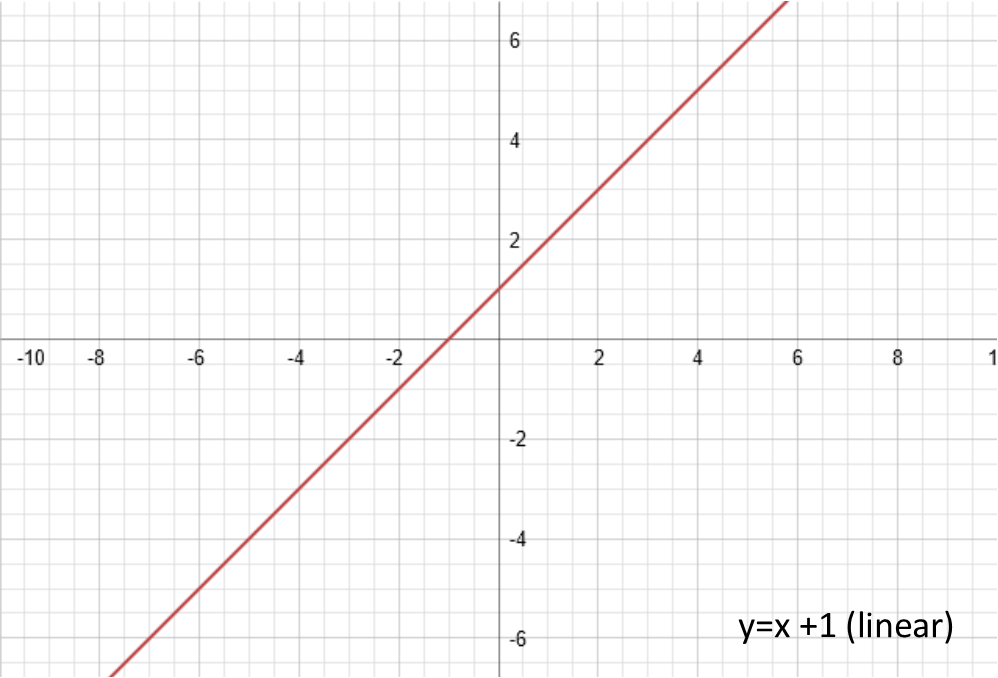
The d at the end of my general form represents a vertical shift in the ouput. It takes the entire function and shifts it UP. Note that this d is outside the function. Which means, since it is addition and not multiplication, it is the last thing applied. When d is positive, it shifts the function upwards. When it is negative, it shifts the function downwards. Here is what the graphs of each of our examples looks like once we add 1 to them (make d be 1):

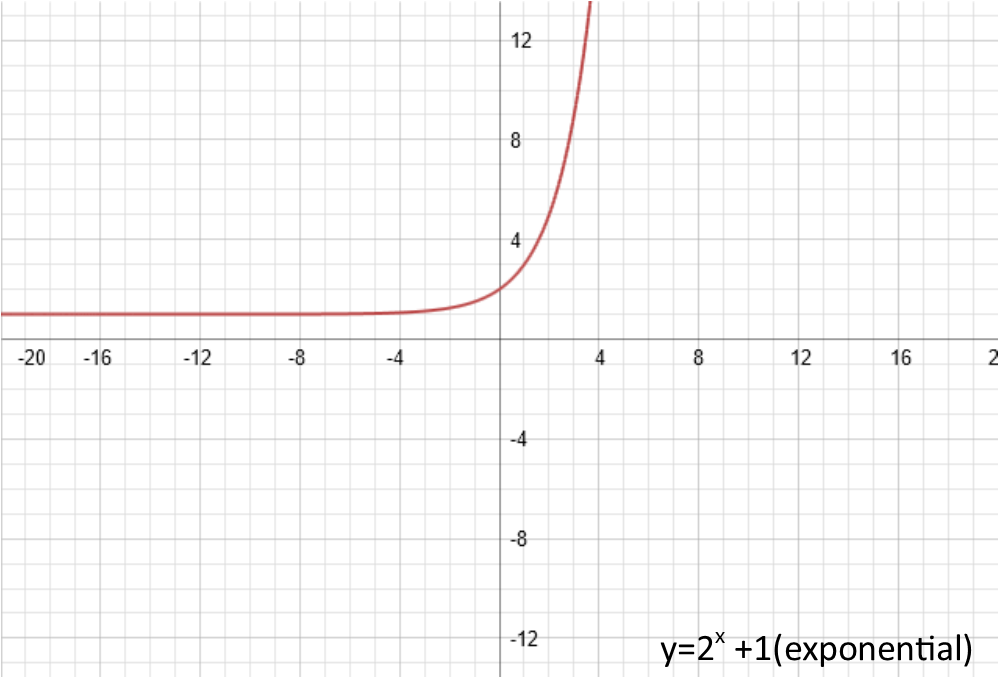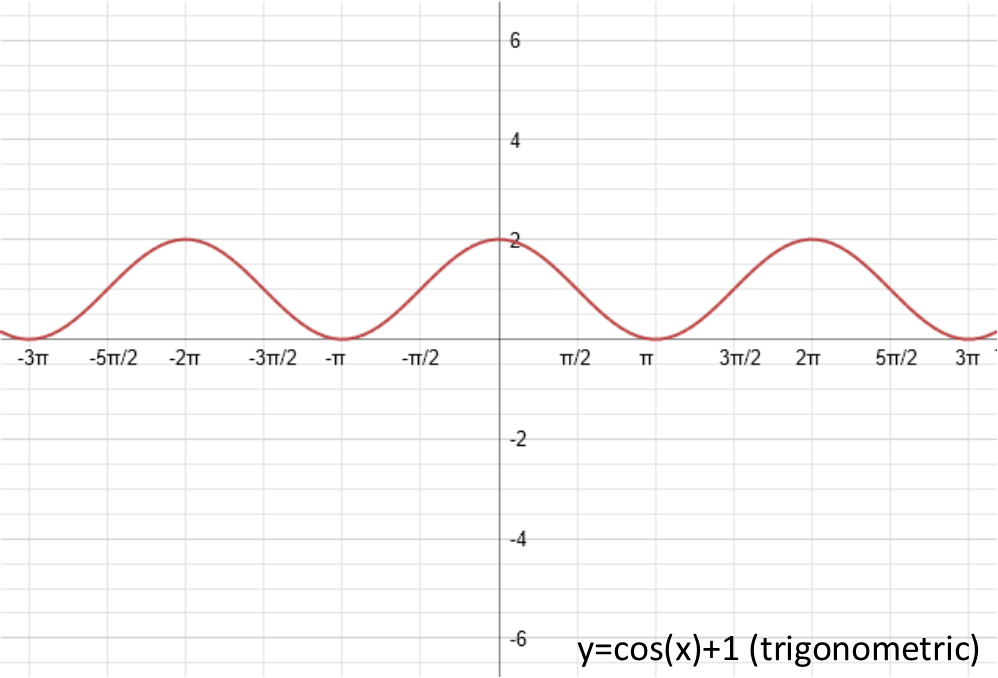
Let’s move on to the a. That represents the amplitude of the function, or as I like to tell my students, the vertical stretch. It doesn’t shift the function, but instead stretches it up and down vertically. The bigger the a, the more the stretch. And if a is a fraction, it will squish it. If it’s negative, it’ll reflect the function around the x-axis (the horizontal axis). Let’s set a = -2 so we can see both the reflection and the stretch:

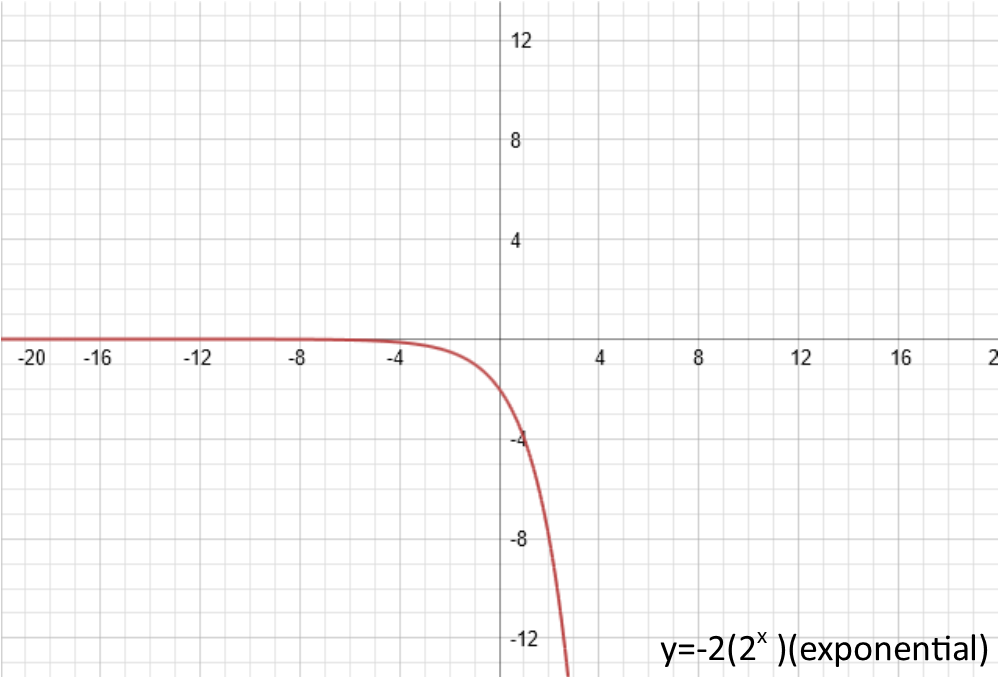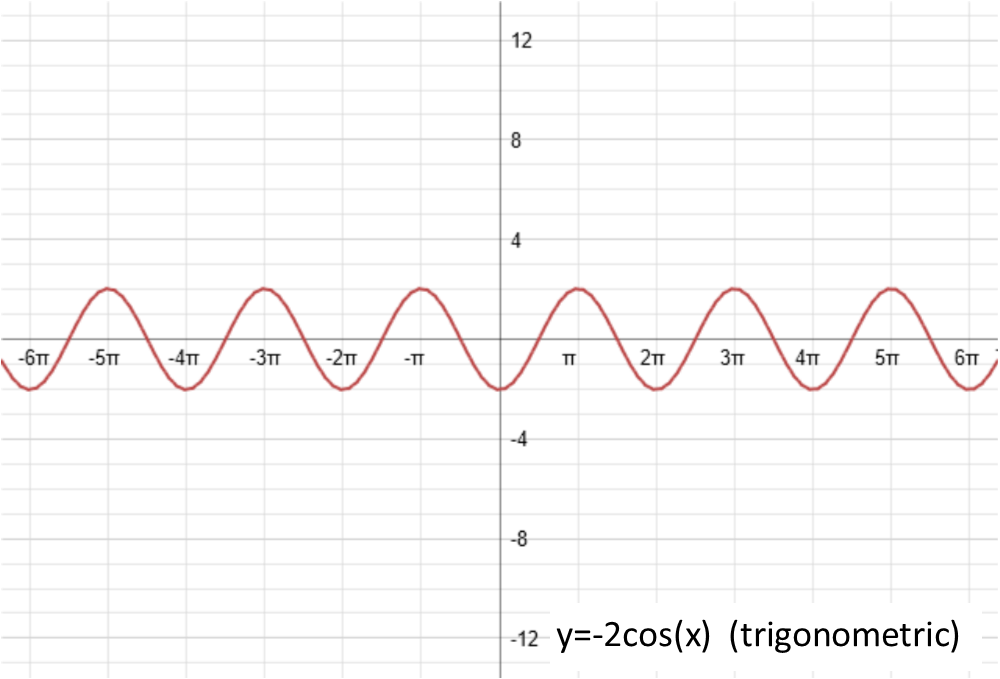
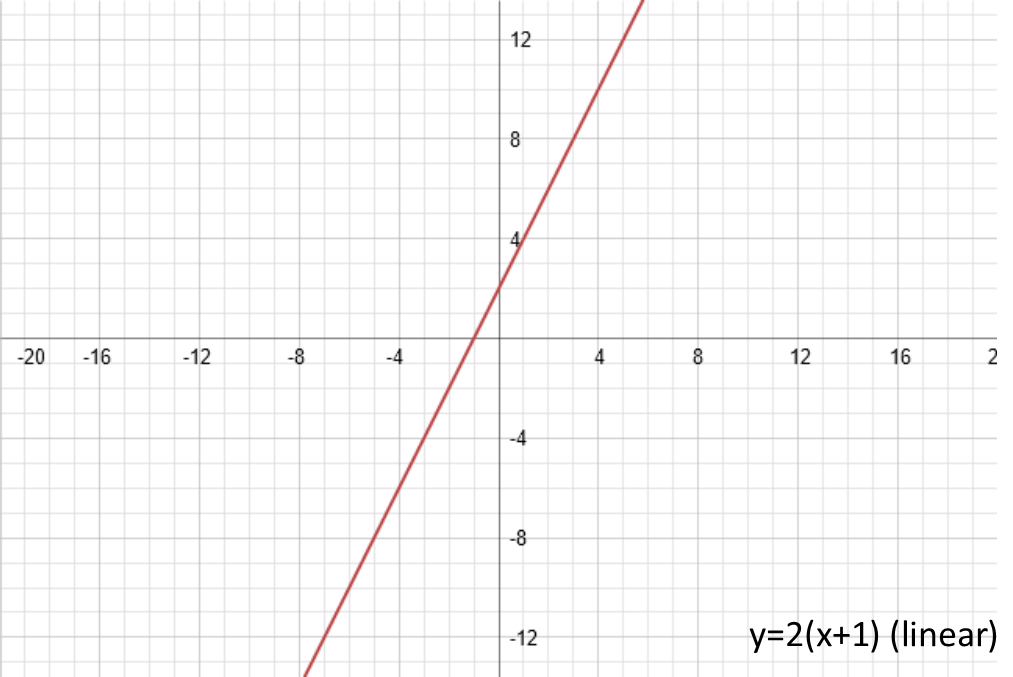
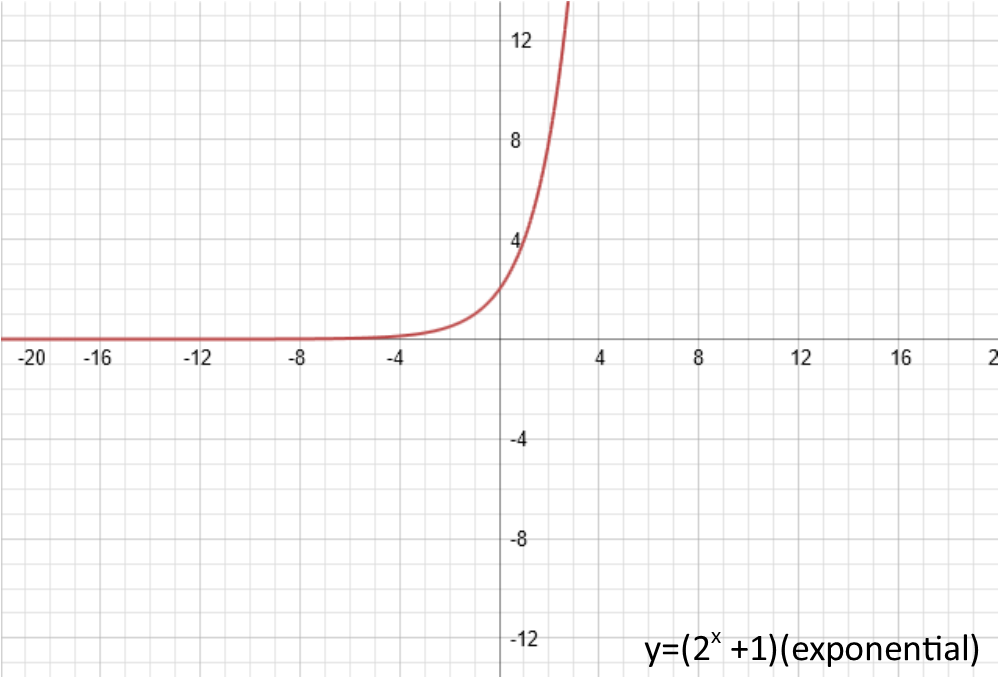
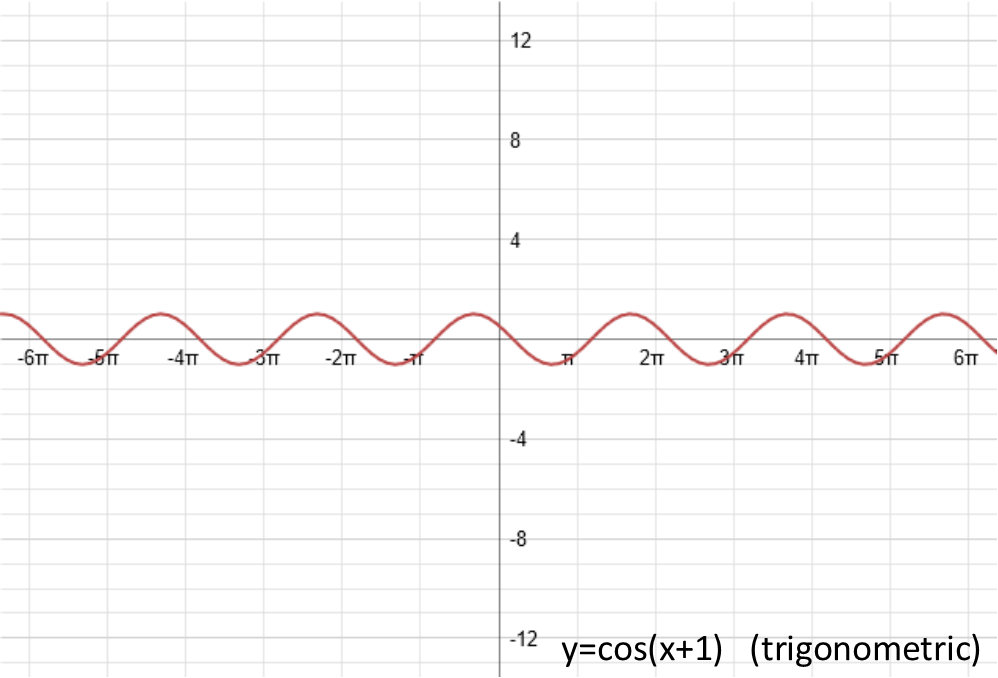
Next, let’s do c. The technical term for c is “phase shift.” What it does, is shift the functions horizontally. If it’s positive, it shifts the function to the left. If it’s negative, it shifts it to the right. If we set it equal to 1, our 4 examples look like this (note that for the linear function, I had to give it an amplitude to be able to demonstrate the phase shift):

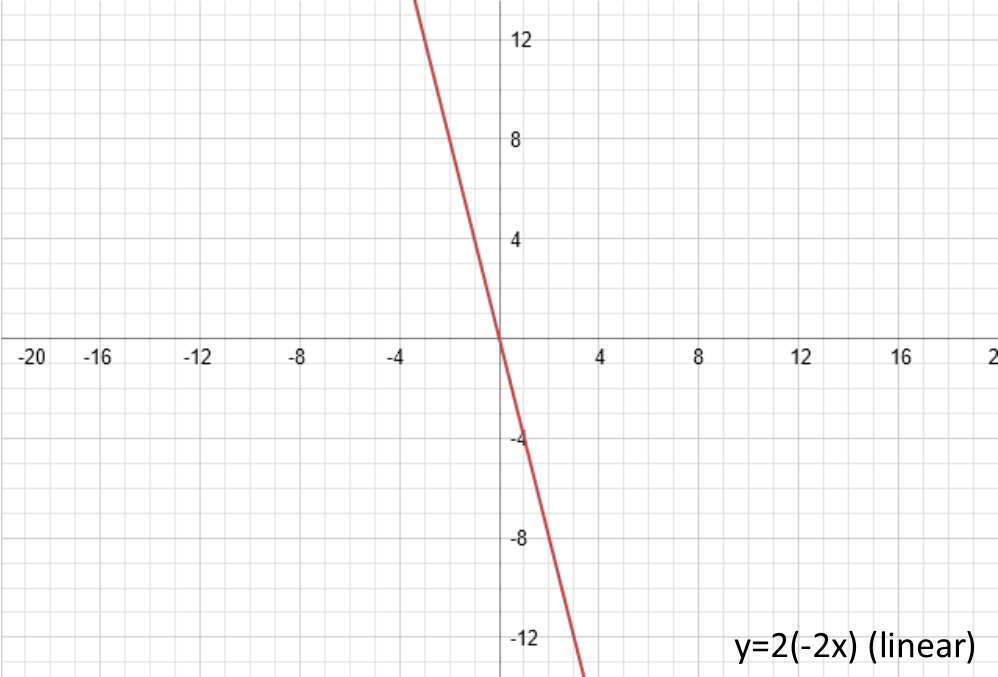
Finally, b. Just like c and d did similar things to the function since their additives, applied in different order, b does something similar to since it’s a multiplicative. B is called the periodicity, or the frequency (depending on what type of function you’re considering), and can be thought of as the horizontal squish. If it’s bigger than one, it squishes the function together horizontally. If it’s a fraction, it stretches it out horizontally. If it’s negative, it reflects the function around the y-axis (the vertical axis). Let’s set b equal to -2 to see both the reflection and the squish. Again, with the linear function I had to give it an amplitude to be able to demonstrate the reflection and squish. Also, note that for both the x² and cos(x) functions, since they are already symmetric about the y-axis, the reflection effectively does nothing.

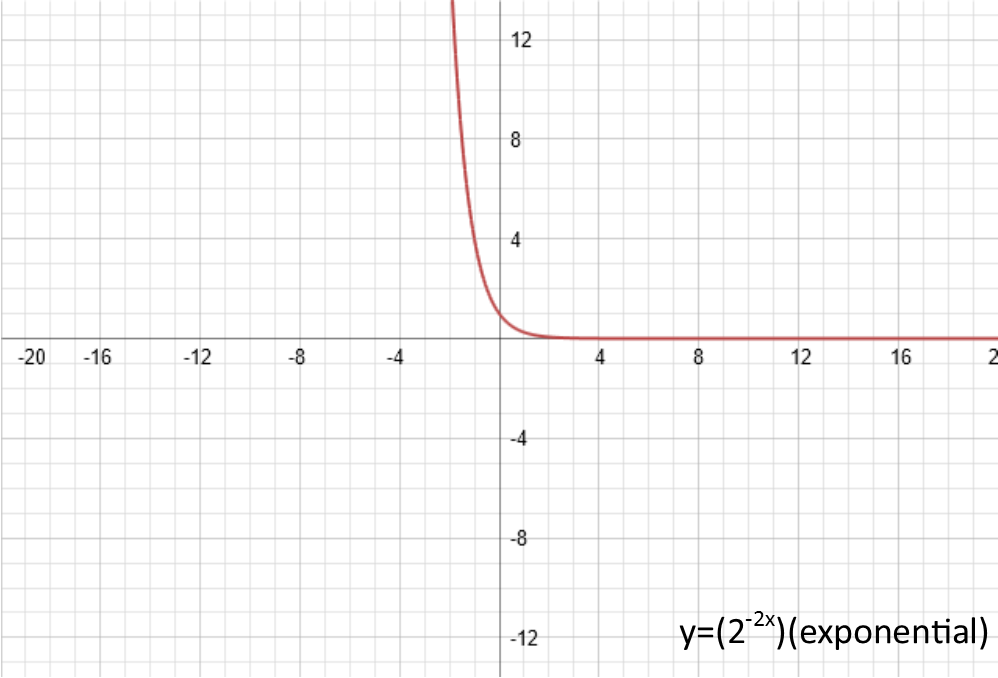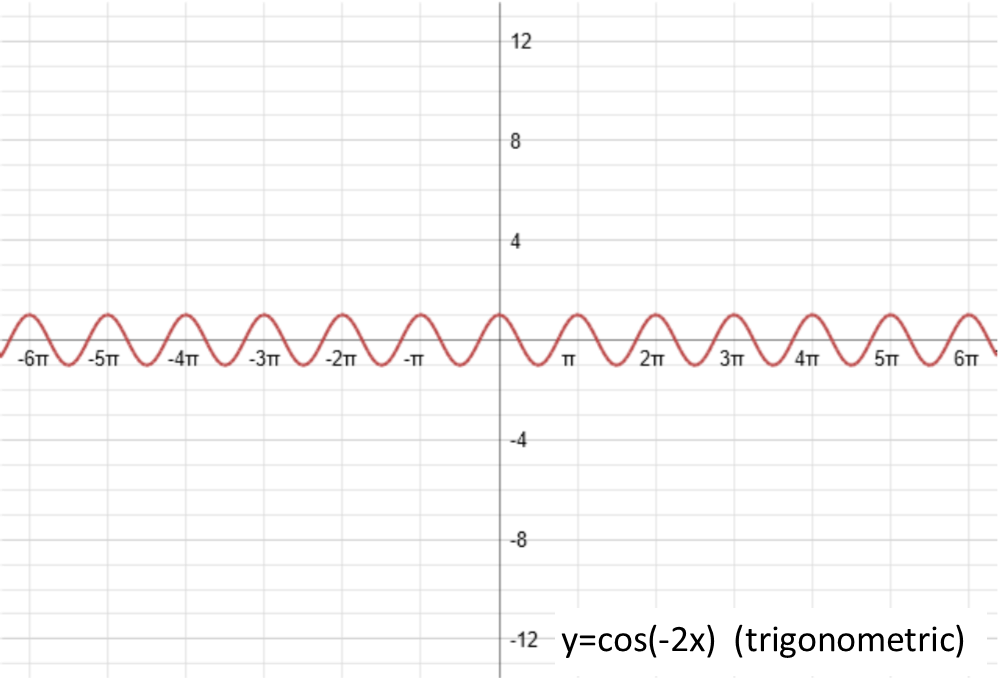
Now, just for grins, let’s put them all together and see what we get. For those x² and cos(x) functions, the reflection will be more obvious now. Also note the interesting things that happened to our linear function when it was reflected about the y-axis and then the x-axis.

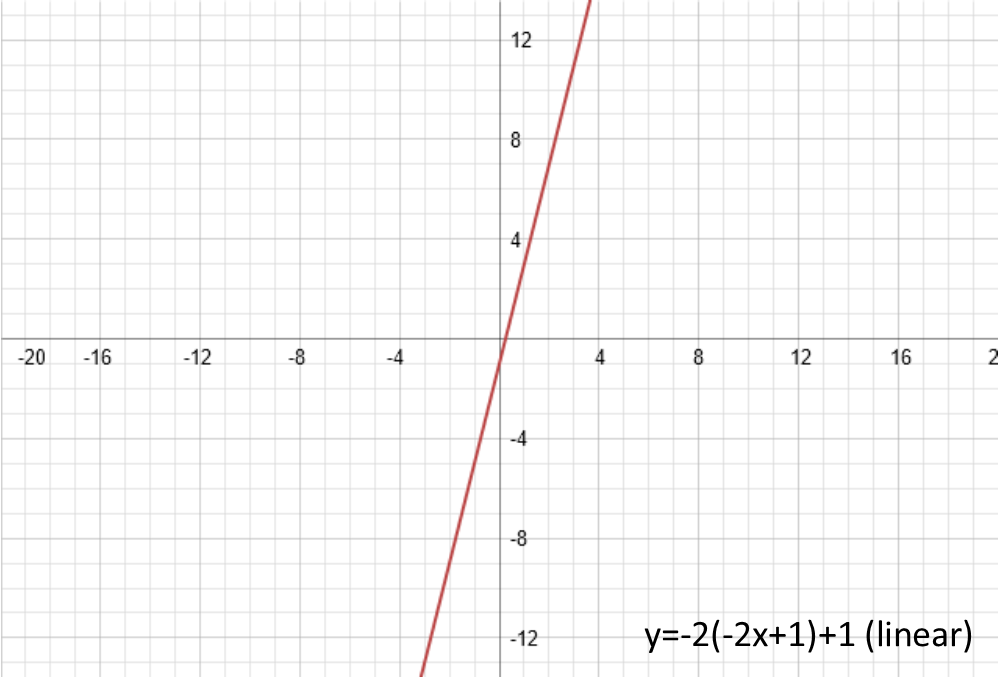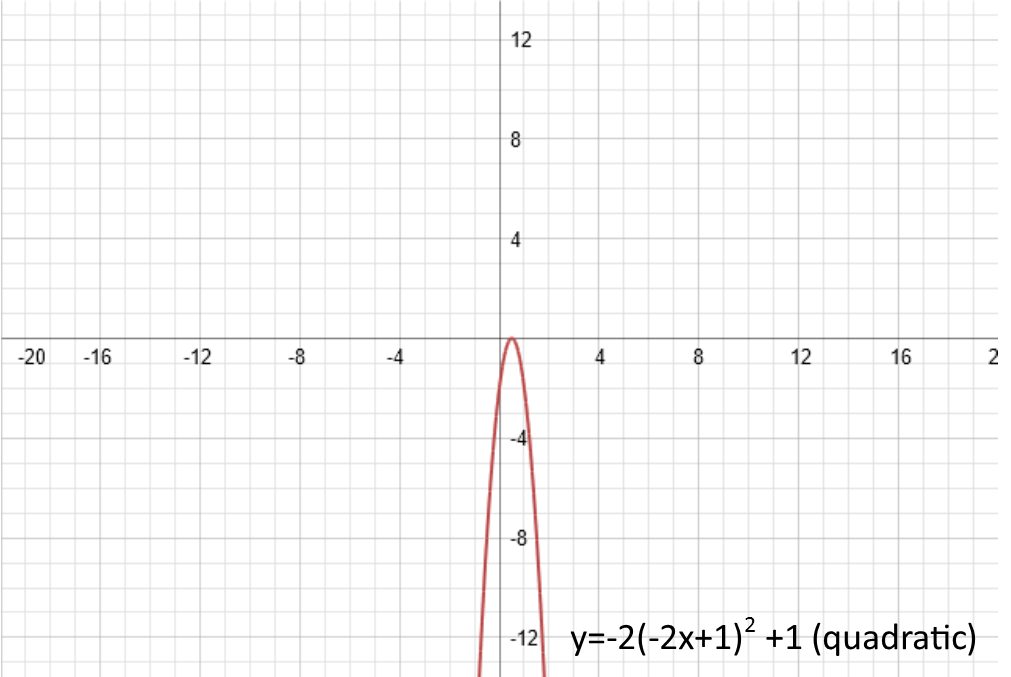
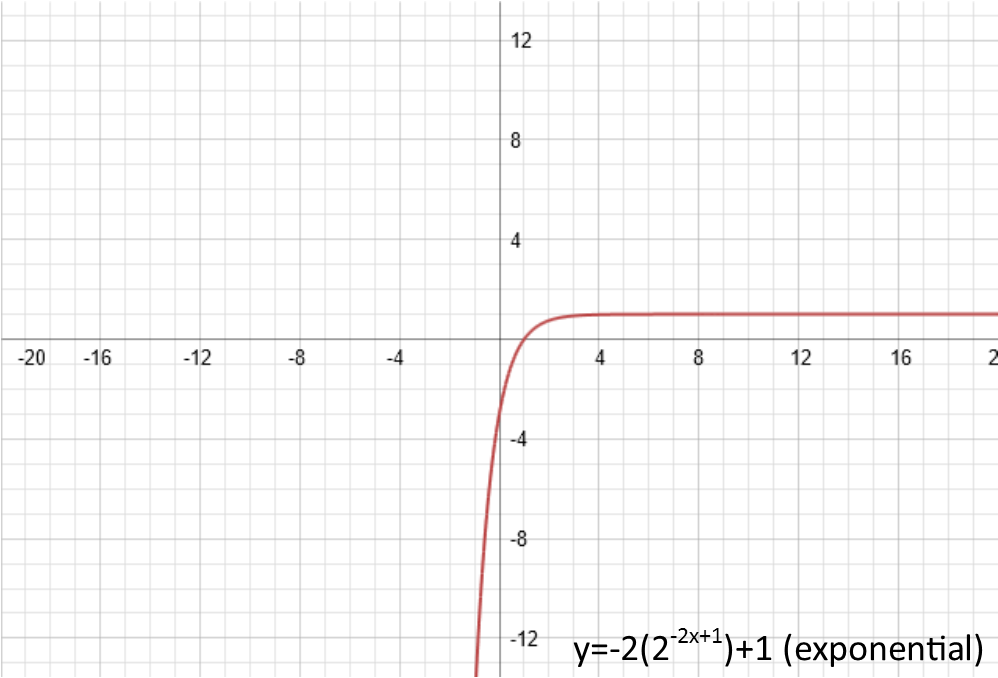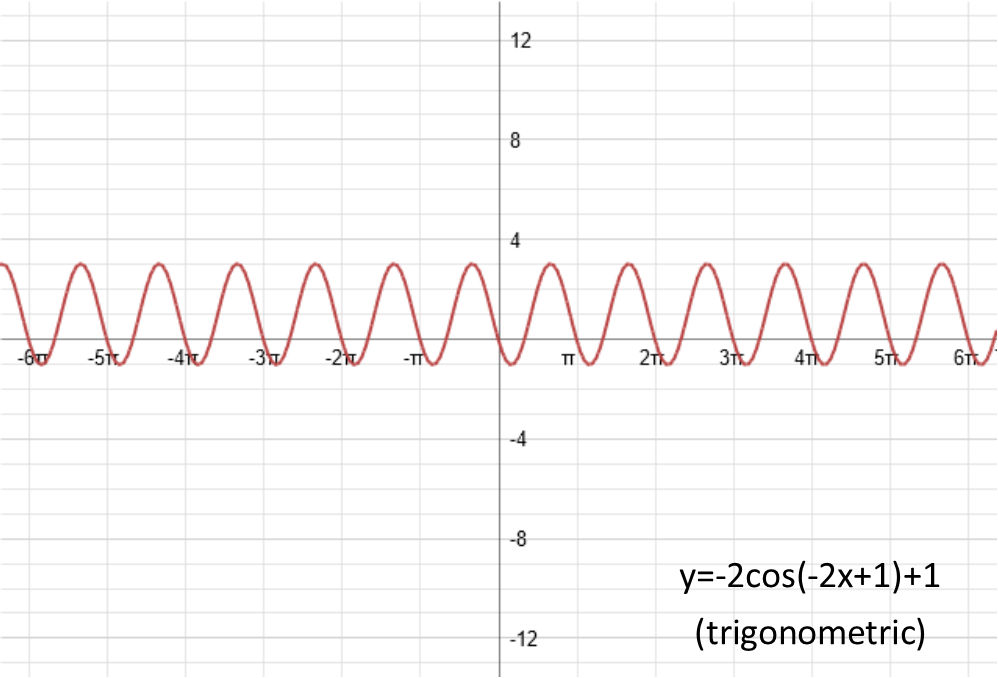
Those are the four things you can physically do to transform any function, without producing a new type of function. (Anything else turns it into a completely different type of function). To recap, they are: vertical shift (added after the function is applied), amplitude (multiplied after the function is applied), phase shift (or horizontal shift, added before the function is applied), and periodicity/frequency (or horizontal squish, multiplied before the function is applied, and before the phase shift is added). So when we look at our functions, we can get a good feel of how it’s being changed.