Math Made Easy: Problem of the Day 1

One of the beauties of mathematics, is that there are frequently multiple ways to approach any given problem, all of which will work. But this beauty also serves as a drawback – some ways will prove far more difficult, or at least time-consuming, than other ways. Couple this with the tendency of many people to go on what’s called “math auto-pilot,” which is letting habit take over and just doing what you’ve always done without thinking, and it is quite easy to waste time on a problem that could be finished much, much more quickly. We see this frequently on some standardized tests, like the SAT, which has problems which are specifically designed to make you waste your time. In this light, let’s look at what I consider to be a great example of this.

Here’s the problem. Try doing it yourself before reading on, where I address the different methods by which you can approach it. If you use the fastest method, you should be able to complete it in under 5 seconds.

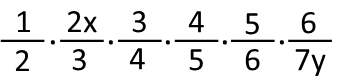
In it, we’re multiplying six fractions. The tendency of many people, especially if they go on math auto-pilot, is to go straight to the multiplication. Let’s go ahead and do this, and see how many steps it’s going to take to finish the problem this way. First, we multiply the top numbers, or the numerators, so we get 2x x 3 x 4 x 5 x 6. Only the coefficients multiply, leaving the variable alone, so we get 720x. In the denominators, or numbers on the bottom, we get 2 x 3 x 4 x 5 x 6 x 7y. Again, only the coefficients multiply, so we get 5040y. Giving us the fraction 720x/5040y.

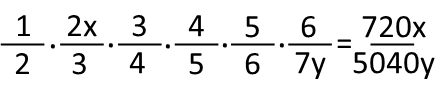
But we’re clearly not done. It looks like we need to simplify the fraction. At this point, you can do one of three things. Some people would do the long division, but that’s going to give a decimal, whose fractional equivalent isn’t obvious. On standardized tests, the answers available for this problem are usually going to be in fractions, so this isn’t a desirable method. We could factor both the numerator and denominator, find the greatest common factor of the two, then divide both by it (resulting in the need for long division again), and get the final answer. This is the MOST time consuming method. The third available is the one I suggest when you’re simplifying fractions, which is to just apply the first common factor that comes to mind for each one, and repeat until you get to the simplest form of the fraction. Here, I simplified first by 2, then 3, then 2 again, then 3 again, then 10, and by 2 once more. There were 6 total steps of simplification this way. Still faster than finding the greatest common factor, but, including the multiplication step, the seven total steps of this method were just far too slow.

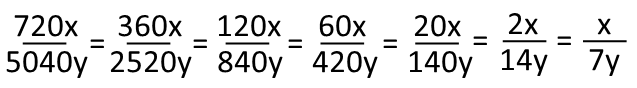
The fastest method, the easiest one, and the one I recommend. SIMPLIFY BEFORE YOU MULTIPLY. I don’t know how many times I have to remind my students to do this, but it will always save you work and time. We remember that, as long as we’re multiplying fractions, when we see a number in the top of one of the fractions multiplied AND in the bottom of one, we can just cancel both of them. Cross the pair out. The two numbers don’t exist anymore. Here, we see 2 paired, 3, 4, 5, and 6. Holy cow, look at that, EVERYTHING cancels except the 1, x, and 7y. Our final answer, with ZERO multiplication, is x/7y (we can ignore the 1 since anything times one is just itself). Doing it this way, you can complete this problem well under 5 seconds, depending on how fast you can cross out numbers.

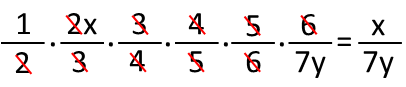
So, that’s it for our problem of the day. Remember to not let yourself go on math auto-pilot when attacking your problems – a second taken to give it a look and think of the fastest way to do it can save you minutes (or more) in the long run.