Math Made Easy: Problem of the Day 100

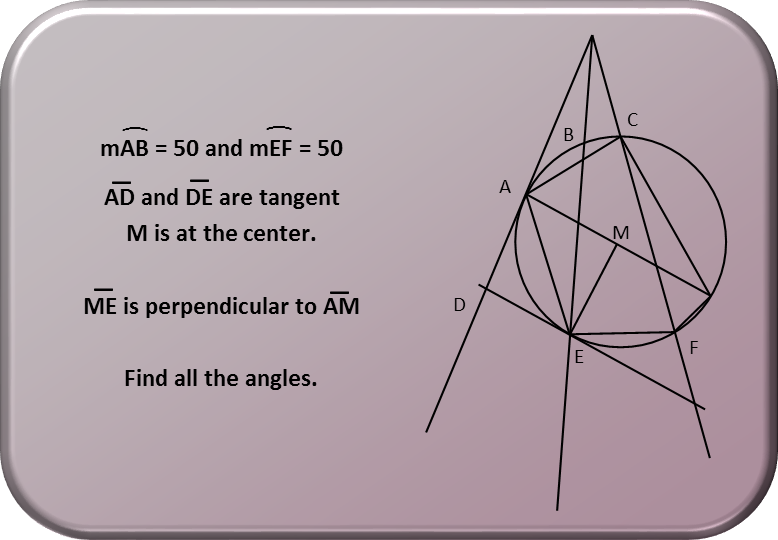
We made it to Problem of the Day 100! Thanks for your continued readership! So today, we’re going to do a geometric puzzle. Which is really what the problem of angles is. There are some simple rules for finding the angles formed by chords, secants, and tangents to a circle. If you use those, and some basic knowledge of triangles and angles, you can solve this readily. Just treat it like the puzzle it is!

So let’s make a new diagram and label all the angles.

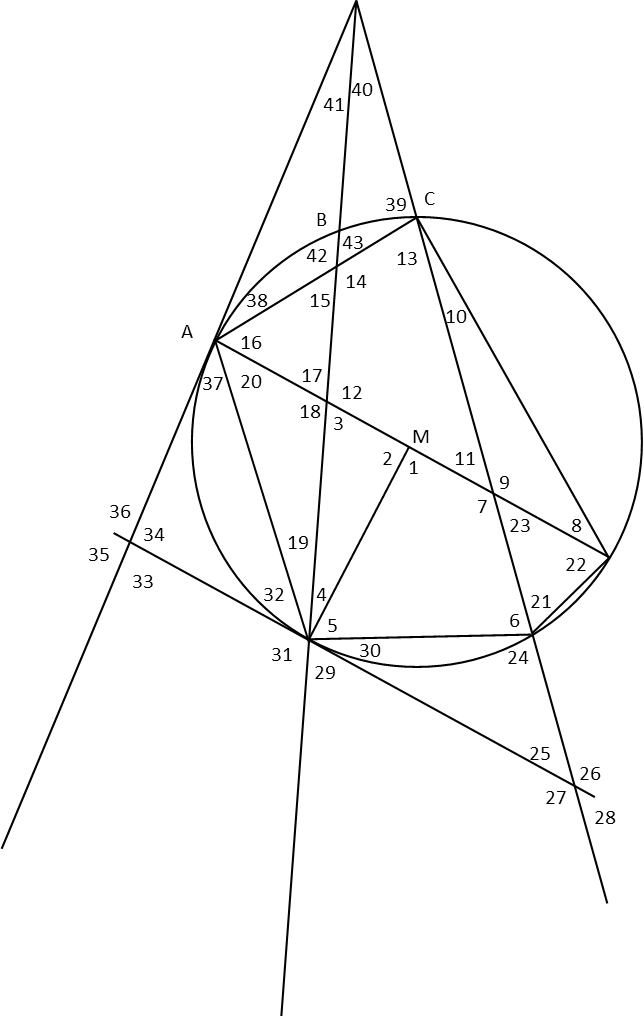
Man, that’s a lot of angles to find. But don’t worry, we’ll start simple, find angles that are quickly determined first, and build from there. You’ll find that, as you do it, it turns into a chain reaction where finding one angle leads to another leads to another.

Now let’s remind ourselves of the relationships of angles to arcs based on which type of lines form the angles.

I’ll make a chart of all the angles, and fill it in as we go. You'll be able to find it towards the bottom of the article

Let’s start with Angles 1 and 2 since they are by definition of perpendicular lines 90 degrees. Angle 20 must be 45 degrees since it is an inscribed angle that intercepts an arc that is also intercepted by Angle 1, which makes that arc 90 degrees.

Angle 19 is an inscribed angle intercepting Arc AB, so it must be half that measure, which makes it 25 degrees. This now gives us two ways to find Angle 18. We can use the fact that it is the third angle in the triangle including it and Angles 19 and 20, or the fact it is an interior angle of two chords, so is half the sum of the two arcs those chords intercept. Those arcs are 90 degrees (since one is also intercepted by angle 2) and 130 degrees (since it is part of a semicircle of which AB is the remainder). That gives Angle 18 a measure of 110 degrees (half of 90+140), and Angle 12 is the same since it is vertical to Angle 18 and therefor congruent. This also lets us quickly find Angles 3 and 17 since they are supplementary to Angles 18 and 12 respectively, making their measures equal to 180-110 = 70 degrees.

Angle 34 intercepts the same arc as Angle 2 and the arc made up by the rest of the circle. That makes it half their differences, so it has a measure of half of 270-90, or 90 degrees. This makes the two tangents perpendicular to each other, so all angles at their meeting are also 90 degrees.

Speaking of perpendicular, Tangent AD has to be perpendicular to the diameter since they meet at the point of tangency. This means Angles 20 and 37 are complimentary. So, subtracting Angle 20’s measure from 90 degrees will give us angle 37’s measure of 45 degrees. Note it’s also made by a chord and a secant intercepting a 90 degree arc, so it’s also half that arc’s measure, which gives us the same result. That also gives us another triangle to finish – Angles 34 and 32 being the other angles in it. So Angle 32 is 180-90-45=45.

Angle 4 we can find by subtracting Angles 32 and 19 from 90, since the three break up the angle of two perpendicular lines. That makes it 20 degrees, and leads us to angle 3 being 70 degrees to finish another triangle, and agrees with what we found for it earlier.

I hope you’re filling your chart in as we go!

Angles 19, 31, and 32 add up to be supplementary – they form a straight line. So to finish the 180 degrees, 31 must be 110 degrees. That means Angle 29 is 70 degrees since it is also supplementary to 31, forming a different straight line with it.

Angle 41 is an exterior angle intercepting a 90 degree arc and a 50 degree arc. As an exterior angle, it is half their difference, and so must be 20 degrees.

Angles 42 and 14 are angles formed by chords, and intercept a 40 degree arc and a 220 degree arc (130 degrees for the remainder of the semicircle plus 90 for the quarter circle). Since they’re formed by chords, they’re half the sum of those arcs, or 130 degrees. This makes Angles 15 and 43, their supplementary angles, 50 degrees. It also allows us to complete the triangle with Angles 15, 16, and 17, revealing Angle 16’s measure of 60 degrees.

And our chain reaction continues. Finding Angle 16 allows us to know that the arc from C to Angle 8’s vertex. It’s measure is twice Angle 16’s. That means Arc BC is 130-120, or 10 degrees, so Arc AC is 60 degrees. Angle 8 is an inscribed angle that intercepts Arc AC, and so is half that, or 30 degrees. Angle 6 is inscribed, and intercepts Arc AC plus a quarter-circle arc, so it measures half of 90+60, or 75 degrees. Angle 24 is supplementary to that.

Angle 38 is comprised of a chord and a tangent intercepting Arc AC, so it has half that measure. If we check the triangle with Angles 38, 42, and 41, we see that agrees.

Angle 25 can be found by the larger triangle comprised of it, Angle 34, and the angle comprised of Angles 41 and 40. That means it measures 180-90-20.

Angle 40 is an exterior angle intercepting arcs of 50 degrees and 10 degrees, so it is half their difference, or 20 degrees. This allows us to find Angle 39 by completing the triangle. Angle 13 is supplementary to Angle 39, and Angle 10 must be complementary to it since they together form the third angle of a 30-60-90 right triangle with Angles 8 and 16. We are now lead to find angle 9 since it completes the triangle with Angles 8 and 10. Happily, Angle 7 is vertical, so is congruent. And Angles 11 and 23 are supplementary to the two.

We can also find Angle 5 since it and Angle 4 constitute the third angle of a triangle along with Angles 40 and 6. So it must be 180-75-20-20 = 65 degrees. Angle 30 is complimentary to Angle 5 since those lines are perpendicular, so its measure is 90-65=25 degrees. Completing that triangle, we find Angle 25 to be 50 degrees, which means its vertical Angle 28 is also 50 degrees, and their supplementary Angles 26 and 27 are 130 degrees.

Only one triangle left. Angle 21 is inscribed and intercepts an arc of 120 degrees, and half that is 60 degrees. So our final angle, 22, is found by completing the last triangle: 180-60-50 = 70 degrees.

We found them all! Hooray!

If you’ve been following on your chart, it should look like this:

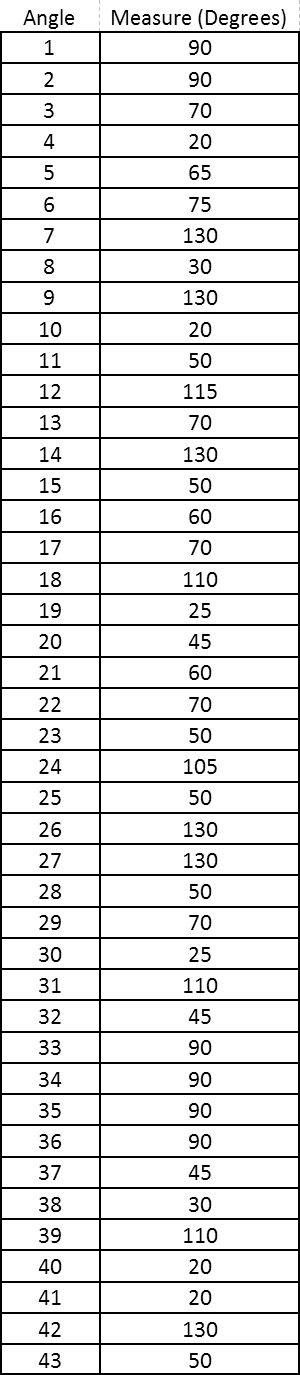
So when your task seems overwhelming, focus on what you *can* do. And keep following the chain. Eventually, you'll find yourself at the end!