Math Made Easy: Problem of the Day 102

Springs are basically force storage devices. As you stretch or compress them, they store the energy, or force, which you used to do so. When let go, they will release as much of that force as possible in the direction opposite their stretch or compression. But they’re never quite perfect, and they don’t exist in a vacuum.

Because of that, we’ll need to make a couple assumptions to be able to do today’s article. Now, recognize, these assumptions are going to make it unrealistic – the toast really wouldn’t fly near that far for several reasons, but without them, we won’t be able to do anything with it.

First, we’ll assume the spring is perfect and delivers all of its stored force to the toast and only the toast. Which means we will ignore friction and any possible side-to-side movement of the springs. We also ignore the mass of the plates on which the toast rests.

Second, we will completely ignore air resistance. For some reason this is magic toast and it slices through the air without any resistance whatsoever. This will have the benefit of us ignoring both the drag the air will put on the toast, as well as any lift the toast might get from the air.

With those two main assumptions, we already know our calculations are going to make the toast go way further than it possibly could. But that’s okay, this is just an exercise to see how we can go from a stored spring force to distance travelled. So let’s start by listing all our known variables. We’ll say that this is some wholesome bread, and that each slice weighs about 50g. We’ll also say this toaster holds two slices and that John wants to launch two slices at a time. He holds the toaster at waist-height, which is around 1 meter. John knows that, for maximum distance, he should aim the toaster at an angle of about π/4 radians (45 degrees). The ground is the final distance in the vertical direction, so we’ll set that to 0 meters. We’ll make the toaster the initial position in the horizontal direction, so that’s 0 meters as well. The x in the spring equation is the distance the handle compresses the spring, or 10cm.

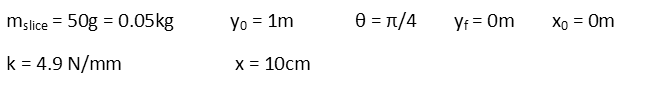
We can easily calculate the force the spring supplies to the toast. We use a simple spring equation for that.

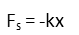
It’s negative, which means opposite the direction of the compression. We plug in our spring constant, k, and our compression distance (converted to mm to keep units consistent):

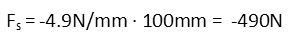
With the spring force known, we can calculate the acceleration it applies to the toast while the toast is in the toaster. For that, we can simply use Newton’s Second Law:

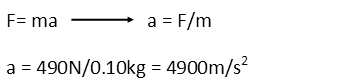
And that leads us to be able to calculate the velocity with which the toast leaves the toaster. We can consider the slots to be kind of like barrels, and assume the spring is providing a constant force the entire time it’s in contact with the toast (it really doesn’t quite, but close enough). So we use one of the kinematic equations where we know our initial velocity (zero since the toast was at rest when the spring released), the acceleration we calculated above, and the displacement distance being the same as the compression distance of the spring.

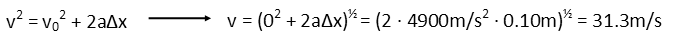
We can already see where our assumptions of no force lost to friction or other variables turn the toaster into a toast cannon.

Now the tricky part. The toast is going to follow a parabolic arc, and end up below where it started. The easiest way to handle this, is to imagine a horizontal line level with the toaster. We can easily calculate the amount of time it takes the toast to arc through the air and hit that horizontal line – we use another kinematic equation, and we recognize that at the point the toast crosses that line, it will be travelling downward at an equal and opposite velocity to its initial velocity upward, since the only force acting on it during that time (with our assumption to ignore air resistance) is the downward force of gravity:

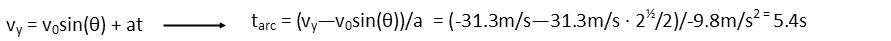
That leaves us needing to determine how long it takes it to fall the remaining distance. To determine that, we need to find its final velocity when it hits the ground. We use the kinematic equation that allows us to equate that final velocity with the initial velocity (this time being the velocity the toast is travelling when it crosses the imaginary line), and its acceleration, again, that due to gravity. After we’ve found that final velocity, we can use the same kinematic equation we used to find the first block of time.

So our total time the toast spends in the air equals the time it took it to describe the arc from the toaster to the imaginary line, plus the time it takes to travel the remaining 1 meter downward.

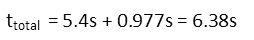
Remember that it is still travelling along the same parabolic arc, we just broke it up into two sections. Doing so lets us calculate the distance it travelled horizontally in one fell swoop. We use the kinematic equation for distance in the x direction, and plug in all the values we’ve found already. The v₀ is the initial velocity as the toast comes out of the toaster. The angle is the angle of the toaster. There is no acceleration in the horizontal once the toast leaves the toaster, so that term is going to conveniently go away, as will the initial x-position term since we deemed that to be zero, as well.

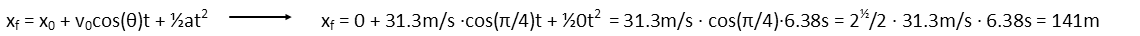
With our assumptions of no resistance and perfect transfer of force, our toast went awfully far! For an added challenge, figure out what the air resistance might be on the toast (you probably will want to assume the toast *doesn’t* flip end over end while it’s flying), and how much that will decrease the distance it travels. You might also want to ignore any lift the toast gains from that air resistance, unless you *really* want to prove your mathematical and physical know-how.