Math Made Easy: Problem of the Day 103

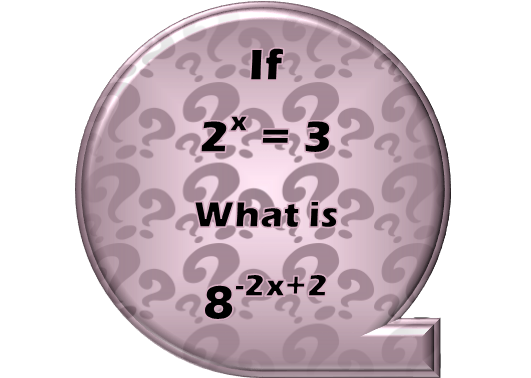
Exponential equations and expressions. The bane of many math students’ lives. They can seem quite intimidating to many. But they don’t have to be. Let’s find an approach that makes this problem easy.

Our goal to evaluate the expression is to manipulate it to the point that we see a 2^x somewhere in it so that we can replace that 2^x with the number 3. To do that, we just take advantage of the way exponents work – all their properties and rules applying to them.

The very first thing you want to do whenever tackling exponential equations or expressions, is to find a common base, if possible. If you can, you will be able to solve it algebraically and not have to resort to logarithms (which may still be useful, but usually the algebraic approach is a bit easier and will get you answers of which you can more intuitively assess the magnitude, or “bigness”). For our current problem, we see we can express 8 as 2³, so that’ll give it the same base as in our given equation. We just replace the 8 with 2³.

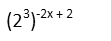
That binomial exponent may look confusing. BUT. A binomial is just adding two things. Let’s think of the rules for exponents. We have three of them – the Product Rule, the Quotient Rule, and the Power Rule. The Product Rule says we should add the exponents. ADD the exponents. A binomial is ADDING two things. So if we do the product rule backwards, we can break up the binomial. Our expression will look like this now:

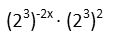
The Power Rule says we should multiply exponents when we raise one exponential term to another power. Let’s do that with the first parenthetical.

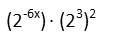
And having down it forwards, can’t we do the Power Rule backwards to separate the coefficient of -6 from x in our parenthetical term 2^{-6x? Just like we used the Product Rule backwards to break up the binomial?}

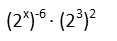
After we’ve done that, we have achieved our goal – we’ve found a 2^x hiding inside the expression. We replace it with three, and just evaluate what’s left. We come out with a reasonable, and intuitively assessable, fraction.

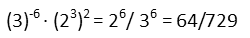
We could have used logarithms to do this, as well. If we had, we’d have gotten a logarithmic fractional value for x, and we could have substituted that into the expression for evaluation. That would have been much uglier, we might have made more mistakes, and we’d still have a logarithmic expression at the end, which would not have been intuitively assessable. The algebraic approach, for this case, was definitely the way to go.