Math Made Easy: Problem of the Day 105

As I said back in Problem of the Day 96, logarithms were invented to simplify multiplication. Namely, they were intended to aid with powers, or exponentials, and are intended as a shortcut for them. But I find, whenever you see a logarithmic equation, I find it best to take two steps: first, if there are any exponents inside the logarithms, bring them out by multiplying the logarithms by them. Second, try rewriting it as an exponential equation and see if you can solve it with algebra (and if that doesn’t work, back up, and continue solving it as logarithms, but usually the exponential equation route will be easier).

For our problem today, we don’t have any exponents to bring out of the logarithms, so let’s just get right down to the process of rewriting it as an exponential equation and solving. Let’s first remind ourselves of how a logarithmic equation relates to an exponential equation. I like to remember it like this:

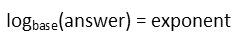
Which means, if we have the following logarithm, we can rewrite it like so:

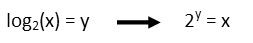
With the one given in our problem, we’ll have to take a couple steps to make it look like the visual mnemonic. To do that, we first need to move the outside 4 to the left-hand side of the equation by subtracting 4 from both sides. Then we move the coefficient by dividing both sides by 2.

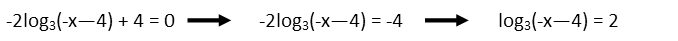
Now that we have it looking like the mnemonic, let’s rewrite it as an exponential equation. We can then evaluate the exponential. Next, we move all the constants to the same side of the equation by adding 4 to both sides. Finally, we multiply both sides by -1 to make our variable positive. And we have our solution.

Our variable x must equal -13.

Hopefully that made the logarithm seem much easier, and not at all intimidating. Many students panic when they see them, but there’s no need to do so. Just take it in steps, and the algebra you already know will solve the problem for you.