Math Made Easy: Problem of the Day 106

When determining the sum of an infinite series, you must first evaluate whether that sum exists. This means we need to determine whether it’s an arithmetic or geometric series. If it is arithmetic, the series will keep getting bigger and bigger (either positively or negatively), and therefor the sum will itself be infinite. If the series is geometric, the sum *might* be finite, but only if the rate of change is between -1 and 1. This will be visible in that each succeeding term of the series will be smaller in magnitude (bigness) than the preceding term.

In our series today, we see that the magnitude of each succeeding term does decrease. This means it is a geometric series, AND it has a finite sum. So we can proceed with our work. Let’s first remind ourselves of how we find the sum of an infinite geometric series. We can use the following simple formula.

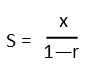
Where x is some number, and r is the rate of change between terms. It can be helpful if we can figure out how to write the series in summation notation to help us better see what’s going on. Our first term is 2, so let’s conjecture that it is our x. To get from 2 to -1, we can multiply 2 by -1/2. The same will get us from -1 to the next term, and to the next. So it looks like our series, written in summation notation, looks like this:

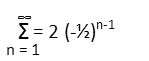
That just leaves us to plug things into our formula. Again, 2 is our x, and -1/2 is our r

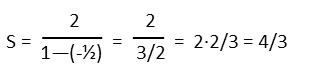
Note that I recognized that 3/2 in the denominator means the same thing as multiplying 2 by its reciprocal, which is 2/3.

The reason the sum came out smaller than the first term is because of all those negative terms. The very first term in the series determines the sign of the sum, since it’s the biggest term. But the second, and all even terms, determines whether the sum is bigger than that first term, or smaller, because they will overwhelm the remaining odd terms. Since that second term is negative, the sum ends up being smaller than the first term rather than larger. Had all the terms been positive, our sum would have been 4 (work it out for yourself if you like).