Math Made Easy: Problem of the Day 107
We’ve talked about unit conversion quite a bit in the articles of the day, but I haven’t yet really demonstrated it. So, to that end, we’ll do a problem solely on conversion of units today.

Unit conversion is really quite simple, which is why so many scientists and mathematicians take it for granted that people just know how to do it. As with most math, there’s an easy way, and a hard way. The hard way is to try to memorize ratios for each type of unit you want to convert between. Since there are a ton of units out there, this can be quite difficult. AND it’s why the metric system was invented in the first place – to try to eliminate the endless variety of ratios one needs to remember to make the Imperial system work.
But what do you do if you can’t remember all the ratios? Well, that’s where the easy way comes in. Just set up the entire thing as fractions, keeping an eye on what you want your end result to be. We want miles per hour, which is mi/hr, so we want our distance on top and our time on bottom. That’ll make our first fraction look like this (note I just added the 60 seconds in the one minute to the 35 seconds):
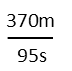
We’re going to multiply that first fraction by other fractions to turn in into the units we want. We’re going to start by adding in a conversion from meters to miles. We can either remember, or look up, that there are about 1600 meters in a mile. We want miles on top in the end, so we need to put miles on top of this fraction.
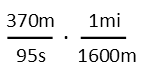
Then we can add in the time conversions. You can do it all at once in one fraction, if you like, or do it in two steps, since we’re going from seconds to hours, which is effectively seconds to minutes to hours. I show it here with two steps. First I add in seconds to minutes. I put the seconds on top so they’ll cancel my seconds in the first time fraction, and because I need the minutes to cancel with the minutes in the second time fraction, which will have hours on the bottom. Which is where we need them to be for our final answer.

Now we can just cancel all the units we can. If we set up the fractions right, we should be left with just the units we want.

Here, we’re left with miles on the top and hours on the bottom, or mi/hr, which is the miles per hour we want.
And the rest is just simplifying the numbers in the fractions. I first see that I have two zeroes in the 1600 on bottom, and two zeroes up top (on in each 60), so I cancel all those zeroes. I also see that I can pull a 5 out of both 95 and 370.
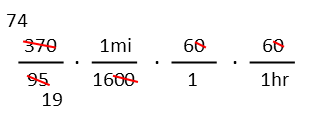
Now I see that I have 3 even numbers up top (74, 6, and 6), and I know I can pull 8 out of 16, which is three 2s. So I cancel all that. It looks like there’s no more simplification that can be done at that point, so it’s time to just multiply and evaluate.

So, if Jorge keeps up his pace, he’ll manage a respectable 8.76 miles/hour (which is a little under 7 minute miles, not too shabby).
Unit conversion is important in mathematics, especially in the sciences. But don’t bother trying to remember all the conversion factors – just do it the way we just did, and any conversion will be simple and easy.
|



