Math Made Easy: Problem of the Day 108

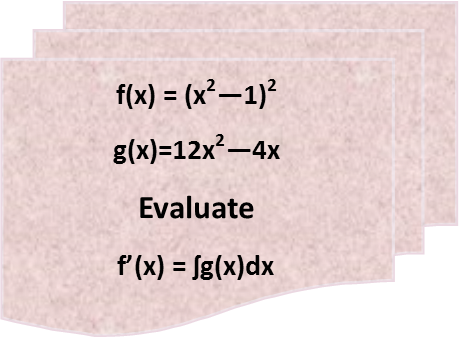
Derivatives and integrals, oh my! Differential equations can be the stuff of many college student’s nightmares, but this one isn’t too bad. In fact, it’s quite on the high school calculus level. Let’s break it down and do it one piece at a time. If we try to put it all together at once and solve it that way, we might make a mistake.

First, we should evaluate the derivative of f(x). It appears to be one function inside another – a difference of squares inside a square. That means we need to use the chain rule. Remember from Problem of the Day 88 I gave a nice, easy way to remember the chain rule, like this:

Using that, we can easily find this function’s derivative. Also remember how you take the derivative of a single term: reduce the exponent by 1, and multiply the coefficient by the old exponent. We apply the chain rule, and then distribute the outside terms.

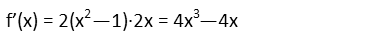
Now to evaluate the integral of g(x). Remembering that an integral is just a reverse derivative, we raise the exponents of each term by one power, and divide the coefficients by the new exponent. Our integral should look like this, with the c at the end representing an unknown constant that we always get when we find an integral.

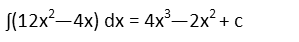
But don’t worry too much about that unknown constant. It actually goes away when we set the derivative of f(x) equal to the integral of g(x). Just, *poof*. So we do that, and we have this:

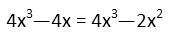
Conveniently, we have identical cubic terms on both sides. They vanish.

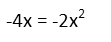
What we’re left with, we can immediately has one solution where x is 0. But if we divide both sides by x, we see it has another solution where x is 2.

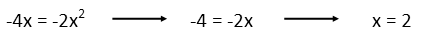
So our solution set is (x=0, x=2).

We see that, by breaking it down and not trying to do it all at once, our problem was actually not all that bad.