Math Made Easy: Problem of the Day 109

Many math problems can be solved conceptually. We can do this one in that manner, but I’ll lay down some of the math behind it just to show exactly what we’re doing.

If Joy is walking in the same direction as the conveyor belt, she adds her speed to that of the moving sidewalk while she is actively walking. So her total speed is just the sum of the two speeds:

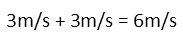
Simple enough so far. Now we could try to set up a system of equations to determine how long she’s on the conveyor belt, but that’s really making the problem harder than it needs to be. This is really about proportions. How much faster is she when she is walking than when she is just letting the sidewalk take her along? Well, set up a fraction of her speed walking over the speed of just the sidewalk.

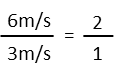
We see she moves twice as fast while she’s walking. She spends an equal amount of time walking as not, so let’s the distance she doesn’t walk x. That means the distance walking is 2x, since she goes twice as faster during that time. Now we can set up an equation (which is really what we’re doing when we figure this in our head) relating the two distances to the total distance, and solve it to find x, or the distance she just lets the conveyor belt carry her.

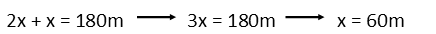
This means she walked for 120m, since that’s twice the distance she didn’t walk. So to find the time she spent doing each, we just divide that distance by her speed.

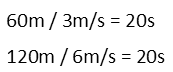
We didn’t actually need to do the math for both, since our condition was that she spent an equal amount of time walking as not (if she walks for half the time, she doesn’t for the other half, so the times spent walking and not walking are equal). That we got the same time for both confirms we did our math correctly. So now we just add the times together.

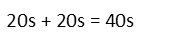
And we see she was on the moving sidewalk for 40 seconds total.

The math of this problem really is fairly simple math. It’s all about concept, and recognizing you can solve it using ratios. While there are other methods to solve it, most of them will be much more work than you need to do. And math isn’t really about making you do work you needn’t do – if that were the case, many of the techniques we have today would never have been invented. It’s more about saving you work. So use the tools you have that will make it easier, and shorter, and faster.