Math Made Easy: Problem of the Day 11

A lot of math problems start when people see something that initially looks more complicated than it is, and panic. They get a brain-lock trying desperately to remember how to do it when what they need to do is pause, take a breath, and remember that all the math works the same, even if there are some funky looking things in there, and that there are often rules to make it simpler than it looks. Today’s problem is one of those cases.

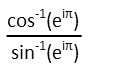
That looks like it might be hard. An inverse cosine with euler’s number with an imaginary exponent inside it? AND pi? All that divided by a similar sine function! Ack! But let’s take a breath, and go through it methodically. Do we see anything that simplifies immediately? We need to think about our trigonometric identities, our logarithm rules, and is there any identity involving e? Why, that last question reminded me that there is! It’s called Euler’s Identity, is a result of applying the Pythagorean Theorem to the complex plane, and looks like this:

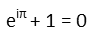
This means that:

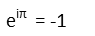
Remembering that the -1 exponent on a trigonmetric function means the inverse of that function, or, in other words, asks the question "what angles returns this value when you apply this function?", and using the unit circle (I’ve got an article on that to help you remember how to build it), we can quickly remember that where the cosine is -1, we have an angle of p radians (or 180 degrees). And where the sine is -1, we have an angle of 3π/2 radians (or 270 degrees). Since working in radians is much easier than working in degrees, I’ll use that:

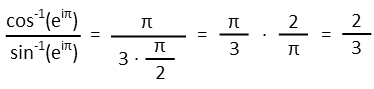
The π’s cancel out, and suddenly our previously intimidating expression becomes the simple fraction 2/3. We didn't even need those trigonometric identities or logarithm rules that we might have been panicking about!

One last thought: The above is true when we keep our angle positive, effectively restricting the domain of sine to 0<x<2π. But if we restrict the domain of sine to -π/2<x<π/2, we get a different result:

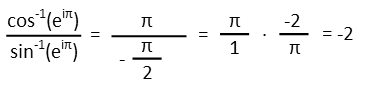
Don’t let your mathematical expressions intimidate you. And remember that trigonometric functions repeat, so restriction of your domain can effect your answer.