Math Made Easy: Problem of the Day 110

Here’s our painter again, always needing help.

Let’s start by diagramming the design. I’m going to break the cross down into rectangles.

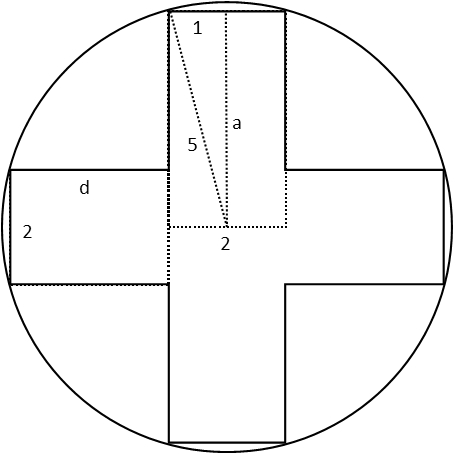
The top rectangle will have a height from its top to the diameter of the circle. This means its diagonal will be the radius of the circle. We can find the height of the rectangle by drawing a triangle with the radius of the circle as its hypotenuse, using the Pythagorean Theorem.

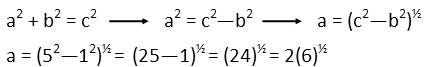
Finding the area of the large rectangle will be easy. Any rectangle has an area equal to its base times its height. So we calculate that.

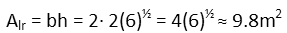
Now the side rectangles. Their length is just the height of the top rectangle minus half its width, as we can see in the diagram that they’re exactly one half width shorter.

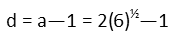
We use the same formula for the area of a rectangle to find the area of the shorter rectangles.

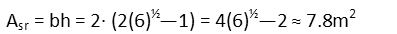
The area of the cross is equal to 2 large rectangles plus two short rectangles. The gold fills the area of the cross, and our painter can only buy whole buckets, so we round up (so he also doesn’t run out of paint before he’s quite done), so he needs to buy 36 buckets of gold paint.

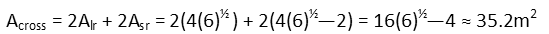
Now we do the circle. It’s easy enough, all we have to do is remember the formula for the area of a circle, plug in our radius of 5, and calculate.

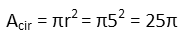
The area of black paint is that of the circle less the area of the gold paint. So we simple find that by subtracting the cross’s area from the circle’s area. And we see it’s almost the same. He also needs to buy 36 buckets of black paint.

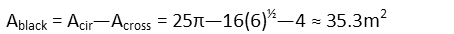
As before with our painter, most problems of geometric areas like this just require you to see the shapes you know how to solve, find them, and find the differences where one shape cuts into another. Do that, and you’ve got it all worked out!