Math Made Easy: Problem of the Day 111

Sometimes I like to say that there’s a certain aspect to physics where it becomes the art of learning what you can ignore and still get a viable answer. That certainly is true. One of the dilemmas physicist face when approaching problems in the real world is there are just so darned many variables, we can’t possibly address them all. So you have to learn which ones matter, and which ones don’t. That can be a case-by-case situation sometimes. Let’s look at a problem today where we have to do just that.

This problem address two things: frictional force, and centripetal force. But they’re really the same thing. The centripetal force is whatever force is providing the acceleration to keep you in the turn. Here, that’s the static frictional force. Static, because once your tires start slipping, you’re starting to lose control of your vehicle. So let’s look at the formulae for both those forces.

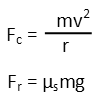
The centripetal force is measured by your mass, velocity tangent to the turn (how fast you would go in a straight line if you stopped turning at any given point), and the radius of the turn. Frictional force is determined by your mass, the coefficient of friction (a constant that relates how strongly two surfaces cling together), and the acceleration due to gravity.

To keep you safely in the turn, the frictional force IS the centripetal force, so we can directly relate those two formulae.

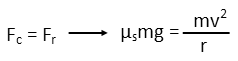
Now here’s where the fun comes in. The fun of figuring out what information is garbage and not needed for our problem. What we can ignore. Notice that the frictional force isn’t going to change from one curve to the next – we’re assuming the road surface hasn’t changed enough to affect the friction, and the truck’s tires hopefully haven’t, either. So that’s the same. So if the frictional force is the same for both turns (since we’re looking for the maximum safe speed for the second turn), then the centripetal force must be the same for both turns.

So we can set the centripetal forces equal to each other. We can completely ignore the frictional force now. We don’t need it anymore. When we set the centripetal forces equal to each other, we see that the mass is the same on both sides of the equation. It can go away, too. *Poof*. We no longer need it, either. In fact, the only thing we need to care about for this problem is the radii of the turns and the velocity of the truck in each turn.

So we now solve for the velocity in the second turn by first multiply both sides of the equation by the second turn’s radius, and then taking the square root of both sides.

We have an equation now that solves for the variable we want, so we plug in our numbers.

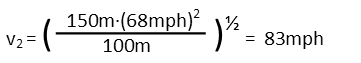
Our driver can accelerate the truck to 83mph before entering the second turn and still make it safely.

The mass of the truck never played into our calculations. We didn’t need it. We could ignore it, and still come out with a reasonable result. Much of physics is just like that – finding out what information you can toss and just not have to deal with it. So if you can master the Art of What You Can Ignore, you can go far in physics.