Math Made Easy: Problem of the Day 112

I seem to be in a physics mood of late, so let’s do some more today.

You might think we need to know the starting velocity of the satellite to determine what its orbital velocity will be. But we absolutely don’t. This is another of those physical situation where we can eliminate factors to come up with a very simple solution.

First, we recognize we can completely ignore the launch of the satellite. It’s already been put in the circular orbit, so there is only one force we need to consider – that which is keeping it in its circular orbit. The interesting thing about a circular orbit, is the object in it is basically always falling. BUT, it’s falling in such a way that it always just misses the earth, making it zip around and around and around (eventually the orbit will decay if no external energy is added to the satellite, but that usually takes a long enough time we can disregard it for this problem).

So the force keeping the satellite in orbit is the force of gravity. Let’s remind ourselves of Newton’s formula for universal gravitation.

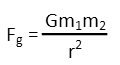
I don’t see a velocity in that formula, so now we need to consider, what direction does that force point? Well, down is the obvious answer, BUT, it also points inwards in relation to the circle the satellite is describing. That means the gravitic force is also the centripetal force. Let’s remind ourselves of the formula for centripetal force:

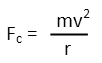
Ah, I see a velocity in that! So let’s set the centripetal force equal to the gravitic force, and then solve for velocity. We first move everything around to get the v basically on its own by dividing both sides by m₁ and multiplying both sides by r, then we take the square root of both sides.

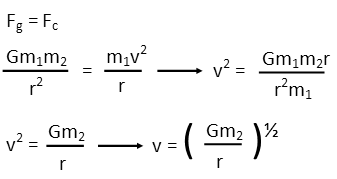
Now we just plug in our numbers and solve. We remember the constant of universal gravitation (or look it up if we can’t remember it), as well as the mass of the Earth, which is m₂. The satellite’s mass is m₁. The only tricky part is the radius – we don’t just plug in the altitude of the satellite’s orbit – we need to add the Earth’s radius to that since the radius of the orbit is from the satellite to the center of the Earth. We can look that up, too, if we don’t remember it. Note that I kept distance is meters for consistency and units in kilograms.

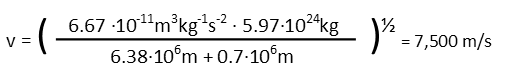
And our satellite is travelling at about 7,500 m/s, which is a little under 17,000 mph. Pretty fast! For an added challenge, see if you can calculate its orbital period.