Math Made Easy: Problem of the Day 113

Every math problem you do should be approached as its own entity. Don’t try to come up with a pat way to handle everything. This is a mistake a lot of students make, especially those who are disinterested in mathematics – they just want a canned solution into which they can plug everything. The difficulty with that is, the world is not a canned place. One strategy may work for one problem, while it might produce a complete nightmare for another. So it’s best to master multiple strategies, and evaluate each problem for which approach might work best for the situation. Let’s look at todays and see what will work best for it.

The very first thing I see in this problem, is that the logarithms all have the same base. This is good, and gives us a nice place from which to start. Then I see that inside the logarithm on the left we have a quadratic. On the right, we have the factors of that quadratic in both logarithms. That’s actually convenient. I further see that there is a sum of two logarithms on the right. The sum of two logarithms is the logarithm of a product. So let’s combine those to reflect that. At the same time, I’ll rewrite the quadratic to reflect that it’s a square of one factor.

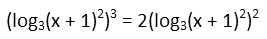
Now we might make one of two different mistakes, or even both. We might try to worry ourselves over how the heck we’re going to cube the logarithm on the left and square the one on the right. We might also be tempted to bring that 2 inside the logarithm on the right, since we know that the coefficient of a logarithm can be brought inside as an exponent. But we don’t need to do either of those, and, in fact, both will just make our math harder. Since the logarithms on both sides of the equation are the same, we can cancel out as many powers on both sides as we can. Since there’s a square on the right, that means we can cancel that square out of both the left and right-hand sides. It just vanishes from the right, and on the left, we’re left with just a single logarithm with no exponent. Now this is very convenient.

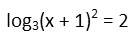
We can now recognize that we can rewrite the logarithm equation as an exponential equation. I like to remember logarithms as being a question, saying “to what exponent do I need to raise this base to get this stuff inside the log?” We can remember the question like this:

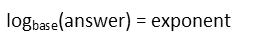
So that means when we rewrite our logarithmic equation, it should look like this:

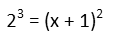
Now let’s evaluate the exponential, and then bring it over to the side of the equation with our quadratic by subtracting it from both sides.

Looking at this quadratic, I can see it’s not factorable, since the only factors of 7 are 1 and 7, and now form of adding or subtracting those two will give us 2. So we need the quadratic formula to find our answer. Let’s remind ourselves of what it looks like.

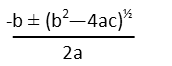
So we just plug in our values and solve. Remember that a, b, and c are just the coefficients, in order. This will give us two answers.

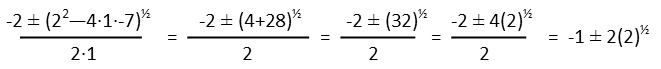
BUT. Remember the Domain we’re given for logarithms – all positive real numbers. Of our two answers, only one will be positive. If we subtract a negative from a negative, we’ll get a negative, so we can toss that answer out. So our final answer is:
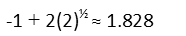