Math Made Easy: Problem of the Day 114

Let’s do some factoring today.

Try to plan your strategy when solving equations. It helps to have an idea of where you want to go before you start doing things. While I often say to try to get all the variables on one side of the equation – and that’s exactly what we want to do – it isn’t necessarily something we want to do right off the bat. With this one, we can see if we do, it doesn’t really help much – we’ll either end up adding all those fractions together, as fractions. Which we can do, since they all have the same denominator, so that’s not too bad a thing to do. BUT, it’ll actually be a little bit too much work. Certainly too much writing. We can actually get rid of the denominators pretty quickly so we’re no longer working with fractions. So let’s do that first. We multiply EVERYTHING by (x + 2). This will cancel out all the denominators:

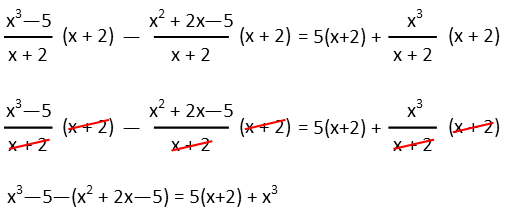
Having done that, notice I put the second fraction’s numerator in parentheses. This is important, because it’s at a step where a lot of students will make a mistake. That minus distributes to everything in those parentheses. If we don’t distribute it, we’ll get the wrong answer. So let’s do that, and then collect all our like terms (all terms with the same variable and exponent).

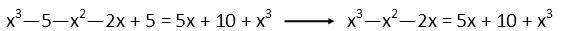
That done, we see there is a cube on both sides with the same sign. It cancels out, so we can get rid of that. Then let’s move all the variables to the same side of the equation by adding the x² and 2x to both sides.

Now we just have a quadratic. And a fairly easy to factor one, at that. Remember that for all polynomials, the possible factors come from the paired factors of the constant. So for 10, our possible factors are 1 and 10, or 2 and 5. Well, 2 and 5 add up to 7, the coefficient of the middle term, which is what we need them to do. So our factored quadratic is:

And that also gives us the answer. We set each factor equal to zero, since only one of them needs to be zero to turn the whole thing into zero. It looks like we have two answers that will work for our equation, as we should for a quadratic.

BUT! Wait, we're not done! Let's look back at the original expression. We almost forgot to consider our Domain. Since x + 2 is in the denominator of all our fractions, this means that x CANNOT equal -2. If it does, we get zero in a denominator, and that's no good. So it is restricted from the domain. That means our equation only has one possible answer, and that is x = -5. So make your plan, and ensure that considering your domain is part of that plan, lest you come to a hasty answer that is incorrect.