Math Made Easy: Problem of the Day 115

Combinations and permutations give a lot of students fits. You only do them briefly in school, usually, so the amount of time spent on them does little to make them seem less strange, or to help take the intimidation out of the formulae and the factorial.

When faced with a problem of combinations or permutations, you first need to ask yourself: “Does order matter in the final result.” In other words, for our problem, do Sally, Joe-Bob and Bassem have to stand in a particular order, or can we shuffle them around? If order doesn’t matter, we’re dealing with combinations. If it does, we’re dealing with permutations. Here, it clearly doesn’t matter where they sit as long as they’re together. A group of Sally, Joe-Bob and Bassem is the same group as Bassem, Sally, and Joe-Bob.

The next question to ask: can any of the items repeat? For instance, you’re getting 3 scoops of different flavours of ice cream. If you don’t mind that two of the scoops are the same flavour, then repetition is okay. For today’s problem, we have three unique human beings, so clearly we can’t repeat. So we should use the formula for a non-repeating combination. We remind ourselves of what it looks like.

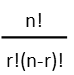
In our formula, n represents how many things there are to choose from – here, the 30 students in Sally’s class. r is how many of them are you going to pick – the three members of the team. So we can plug in our numbers and do the little bit of subtraction in the parentheses.

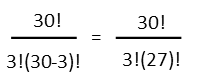
Now to deal with the factorials. A factorial is just that number times every single number smaller than it in a big long chain down to one. So 4! Is: 4x3x2x1. But don’t just multiply them out, or go reaching for that calculator! A lot of this can be done without it! Write out the whole factorial, and then find all the like numbers top and bottom, and just cross them out. Poof! They’re gone!

Now that we’re down to fewer numbers in the fraction, we can finish simplifying. I see the 3 goes into 30, so we cancel and reduce there, and the 2 goes into 28, so we do the same. There are 4,060 possible 3-person teams in that class of 30 students.

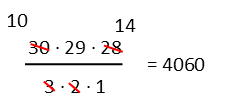
But Sally only cares about the team that puts her with her friends Joe-Bob and Bassem. That’s only one of those 4,060 teams. So we calculate the probability by putting the desired outcome over the total possible number of outcomes.

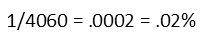
Hrm. 0.02% really isn’t very good odds. Sally doesn’t like that. She probably won’t end up on a team with BOTH of her friends. Well, that’s what happens when things are left up to chance.