Math Made Easy: Problem of the Day 116

No doubt on when you take the SAT, ACT, or even the GRE, you’ll run into a problem like this one. They’re very fond of problems where you need to find a few different integers given certain described relationships of those integers. It tests your number familiarity as well as your understanding of a few fundamental math concepts.

This one is all about recognizing that, since we’re given equivalencies, or ratios, of the three numbers, we see that all three are factors of a bigger number. And the coefficients of each in the equivalency are also factors. But we don’t need a, b, or c to find that bigger number. All we need to do is multiply the three coefficients. If we get that, we know the number. So let’s do that first.

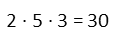
Now that we know we have an expressions 30 = 30 = 30, we can set in turn each term equal to 30 and solve to find a, b, and c:

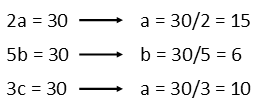
Remember, what we just did worked BECAUSE all these numbers are factors of 30.

And now we just plug a, b, and c into our expression in the question to find our answer.

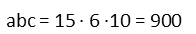
Now, as often is the case in math, there is another way to do this. One could recognize that the given equation is really a system of three equations. One could set it up as such and solve the system of equations accordingly. But that really is a lot more work than would be necessary, and we really do want to save ourselves as much work as possible, no? Especially on a standardized test where we’re under a time crunch.