Math Made Easy: Problem of the Day 117

Sound can do some interesting things sometimes. As wave phenomena, sounds waves can enhance each other (and even themselves) or interfere with each other (and even themselves). This problem has a little bit of both going on, and just takes a moment of thought.

When we consider that the first sound is making the glass hum, we must recognize that its wavelength is in resonance – it means the wave is just the right length to fit inside the glass. So the diameter of the glass is the same as the wave’s length. That means our sound wave has a wavelength of 10cm. We can find it’s frequency by reminding ourselves of the wavelength formula and solving it for frequency.

In that formula, the Greek letter Lambda is the wavelength, v is the velocity of sound (we’ll use the velocity of sound at 20° Celsius, which is about 343.2 meters per second), and f is the frequency of the wave. Once we have our formula, we plug in our numbers.

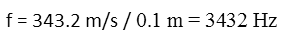
Now that we know its frequency (in between an A7 and an A7 flat – just toward the end of what a piano can do), we can consider the beat frequency. A beat frequency is a phenomenon that happens when two sounds have similar, but not quite the same frequencies. They have to be very close for it to occur, and when they are, a beat can be heard caused by the two waves interfering with each other. And the formula for finding that is very, very simple. We simply subtract the lower frequency from the higher, and you have the beat frequency. But since we have the beat frequency but not the higher wave’s frequency, we set up the formula and solve for it.

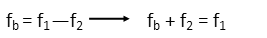
Then we plug in the frequency we found for the first sound and the beat frequency of 5 beats per second (which we can also call Hertz).

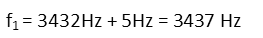
And we have the frequency of the second speaker. This problem really only required remembering one formula and a couple concepts – the beat frequency “formula” is really something you can just derive by considering what the phenomenon is, so you don’t actually have to remember it.