Math Made Easy: Problem of the Day 118

Pew! Pew! Pew! Let’s get relative today! In movies and science fiction, we’re always more fascinated by energy weapons than mass driver type weapons. We generally consider them to be more advanced and more destructive than the mass drivers could be. But are they really? This problem addresses just that question.

As always, let’s tackle this in parts, starting with the simplest and work our way towards the hardest. We don’t need to do any transformations to calculate the kinetic energy of a photon, since its velocity is invariant regardless of the inertial frame of reference. In other words, the speed of light is the same to the people on the spaceship and the people watching it from afar – it doesn’t matter that the laser was shot from a moving spaceship. The ship’s speed adds nothing to the speed of light. We also note that the kinetic energy of a photon is the entirety of its energy. So we remind ourselves of the formula for the energy of a photon based on its wavelength:

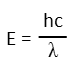
This is nice and simple. Given that it’s violet, we have a good idea of its wavelength, since that is what determines the colour of the light. We know the speed of light, and h is Planck’s Constant. Let’s jot all those down right fast.

Now that we’ve noted all our values, we plug them into our equation and we get the energy of the laser’s individual photons.

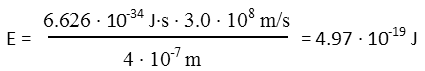
Now for the kinetic energy of the electrons being fired. Since electrons are massive particles, the gun is basically a mass driver. It’s firing them at relativistic speeds, so there are a few things we need to consider before we dive blindly in and assume the kinetic energy of the electrons is just their mass times their velocity squared, as they would be in a Newtonian frame of reference. If we did that, we would be very, very wrong for a few reasons. Let’s walk through it to see why.

Einstein told us that the energy of a particle is equal to its mass times the speed of light squared. Just about everyone knows this, even if they don’t have much of a scientific background at all. Pop culture won’t let us NOT know it. But is its mass invariant? Does the mass change as the particle accelerates towards the speed of light? Well, to an outside observer, it actually does. So we need to account for that change based on its velocity, which means its energy changes, to the observer, based on that velocity relative to the observer.

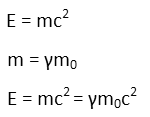
This allows us to calculate the relativistic kinetic energy of the electrons. It’s simply the difference between their observed mass-energy and their resting mass-energy. A quick factoring of the resting mass out of the accelerated mass gives us a formula using only the Lorentz Factor (γ), the resting mass (m₀), and the speed of light.

Let’s remind ourselves of how we find the Lorentz Factor.

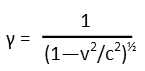
Oh, wait, that includes the velocity of the particle relative to the observer. BUT. What *is* that velocity? We’re not given it straight away – just the electron’s velocity relative to the ship. Our human intuition tells us we should just add the ship’s velocity to the electron’s velocity relative to it – that makes sense, if I throw a ball off a moving truck, the ball has the speed I threw it plus the truck’s speed. But that’s a low velocities – on the Newtonian scale as we scientists like to call it. But at relativistic speeds, we can’t do that. It wouldn’t even make sense here, because that would mean the electrons are going faster than the speed of light, and the universe won’t allow that – nothing can go faster than the information carrier that tells us how fast the thing is going, and that information carrier is light. So we need to calculate the relative velocity of the electrons, as the observer sees it. We can use the following transformation to do that:

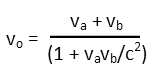
Plugging in our velocities (it doesn’t matter which is v_a or v_b), we see those electrons are moving at a whopping 91% the speed of light.

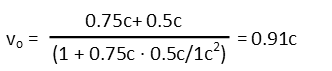
Now we can calculate our Lorentz Factor.

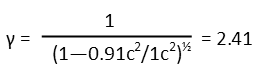
With that, we remind ourselves of the measured resting mass of an electron, and plug everything in to find our electron’s kinetic energy.

Holy mother of goose eggs! That electron has WAY more energy than the photon. Six orders of magnitude more. We needn’t even both subtracting to find the difference. The electron has so much more energy than the photon that they’re not even in the same ballpark. Six orders of magnitude is practically one million times more energy.

So why are energy weapons so crazy popular in science fiction when mass drivers can be shown to deliver much more energy per particle? Well, mostly because they're exotic, they sound fancier, and, on the screen, are much prettier - flashier. We can make shiny colourful lasers or beams or what-have-you. But the mass driver… will be mostly invisible, because the particles are moving so fast we can’t track them, or they’re subatomic, so we can’t see them. At best you might see some sparklies as they interact with and annihilate dust particles in their path. There’s also the belief that energy weapons might be more energy efficient than mass drivers – after all, it does take quite a bit of energy to accelerate a mass to those relativistic velocities. BUT, once you do, the mass is far, far more devastating than the photon.