Math Made Easy: Problem of the Day 12

Today’s problem is all about factoring and recognizing domain restrictions.

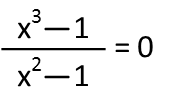
Normally when we solve polynomials, we factor them and recognize set each factor equal to zero to find its roots. Rational expressions, which are fractions with polynomials in the numerator and/or denominator, create another step we must do while finding the roots. We still start by factoring all polynomials in the expression, noting that on top we have a difference of cubes and on bottom we have a difference of squares, like so:

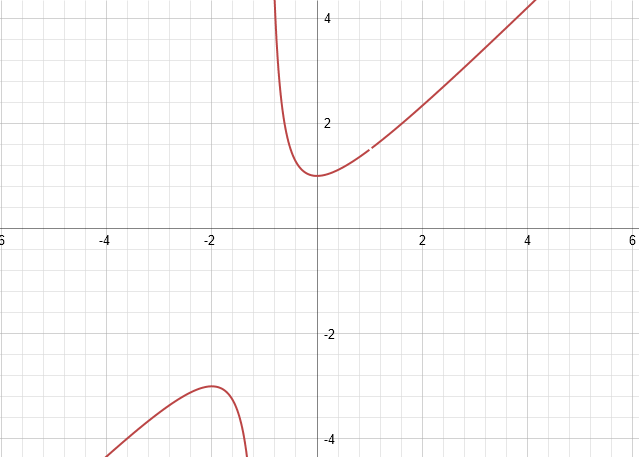
Now it might be tempting to simplify the fraction next. There is obviously a root in both the numerator and the denominator we can cancel. BUT! Before we do that, we must consider the roots in the numerator – they restrict the domain, or all possible values of x. It does so because we simply can’t have zero in the denominator. Doing so makes our math implode, and, when one considers the physicality of it, what it means to have zero in the denominator, it doesn’t even make sense – how can you divide by zero? If I tear a sheet of paper in half, I have divided it into 2 parts. But there is no means by which I can divide it into no parts. So dividing by zero makes no sense, therefore, we cannot allow any values of x which produce a zero in the denominator. So for this expression, the values -1 and 1 are disallowed. The function, when graphed, simply doesn’t exist there. As we see in this graph of the expression (not the whole equation, I just graphed the rational expression here). Note the vertical asymptote at x=-1, and the hole at x=1

So now we can simplify the fraction. We eliminate those common roots. Can we factor that quadratic up top? No. It’s not factorable, which means our fraction is also in its simplest form. We can now basically ignore the denominator, since we know it can’t equal zero. So anything that produces a zero up top, that is not 1 or -1, will solve our equation. So to solve, we now need to use the quadratic formula.

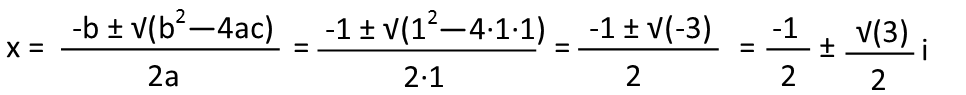
And it turns out we have two answers, both of which are complex numbers. The equation has no answer in the domain of real numbers, but I didn’t restrict us to that domain, so we can be happy with our result of two complex numbers.

So the lesson from this problem: Remember to check your domain restrictions before you accept all roots as your answer. Had we not done so, we might have been tempted to add 1 and maybe even -1 to our set of answers, when our expression simply can’t exist there.