Math Made Easy: Problem of the Day 120

The dot product and cross product give us two very different results. The dot product gives us the magnitude, or length, of the projection of one vector onto another (sort of like it shadow on the other vector). The cross product produces an entirely new vector – one that is perpendicular to the other two vectors, and whose length is equal to the area of the parallelogram we’d draw if we made one from the original two vectors. They both have their uses in mathematics and physics, and can both be viewed as different kinds of multiplication. Because they give different kinds of results, we can’t compare the two directly, which is why today’s problem asks about the magnitude of the cross product, rather than that new vector itself.

So let’s tackle it and see what we get. Is the shadow of the first vector on the second longer than the perpendicular vector? That’s what today’s question is asking. Keep in mind, that if we get a negative answer for a dot product, all that means is what direction the shadow is pointing. So if we’re comparing size, we ignore the negative sign.

To find a dot product, we simply multiply the like components of the two vectors, and add them. Doing this with our given vectors, we arrive at the following:

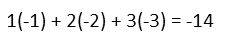
So, since our answer is -14, the shadow has a length of 14, but it’s pointing in the opposite direction of the second vector. We’ll just consider it’s “bigness” to be 14 for comparison to the cross product’s vector.

To find the cross product, we’ll be producing a new vector. Each component is equal to the difference of the products of the other parts flip flopped. This can be kind of confusing, so think of it this way: for the x component, we multiply the y of the first vector times the z of the second vector and subtract the product of the y of the second vector times the z of the first. Like so:

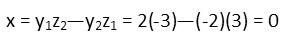
And we repeat the process in the same way for the other components, remembering that what we’re multiplying and subtracting are the parts other than the component we’re currently finding.

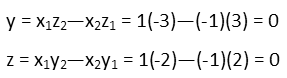
So this gives us the vector:

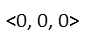
That vector obviously has a magnitude of zero, but to prove it, we just square the components, add them, and then take the square root (it’s basically the Pythagorean Theorem):

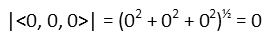
The cross product of those two vectors has no length at all. So their dot product is bigger. The cross product also tells us that the two vectors are parallel. If their dot product had been zero, we would have known they were perpendicular – those are two more uses of the dot and cross product – they give us an idea of the orientation of the two vectors relative to one another.