Math Made Easy: Problem of the Day 121

A good test of your math skills are situations that require you to relate one type of measure to another. The tendency is to think we can only deal with problems of area or volume or whatnot if we’re given hard information – measures of the height or radius, or length, or what have you. But the truth of the matter is, the constraints are more than enough to enable us to find what we need. All we need to is consider the relationships involved.

Let us start with the cylinder. We know the formula for the volume of a cylinder. If we’ve forgotten the formula for the surface area, we can recognize that it has two circles – one on the base and one on the top. Those both contribute to the surface area. And the rest is the product of the circumference of one of the circles and the height of the cylinder. So just add it all together. Writing down our formula to remind ourselves of them, we have:

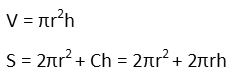
Since the volume of the can has the same magnitude as the surface area, we set them equal to each other, and solve.

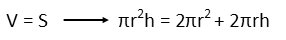
We note that there is a πr in all three terms, so we just cancel that right out.

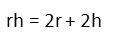
We then move all the r terms to the same side of the equation via subtraction.

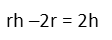
Seeing that we can factor an r out of both terms on the left, we do so.

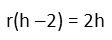
And we then divide both sides of the equation by (h - 2) to isolate r, giving us an expression of r in terms of h.

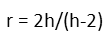
Now to do the same with the sphere. We first remind ourselves of the formulae for the volume and surface area of a sphere.

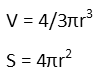
We then set them equal to each other.

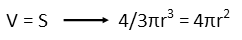
We note that both sides have 4πr² in them, so we cancel that right out. Conveniently, this equation has almost solved itself. We just multiply both sides by 3 to finish, and we have a set number for the radius. It is ONLY when the radius of a sphere is 3 units that the volume and surface area will have the same magnitude.

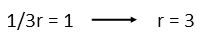
So now we go back to the expression for r in terms of h we found for the cylinder, and plug in 3 for the radius, and solve.

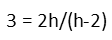
To do so, we first move the (h - 2) parenthetical to the left-hand side by multiplying both sides of the equation by it.

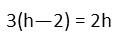
We then distribute the 3 inside the parentheses.

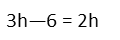
Now subtracting 2h and adding 6 to both sides at the same time, we arrive at our set value for h. It MUST be 6 units. Nothing else will allow the surface area of the can to have the same magnitude as its volume.

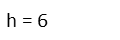
And since we were asked for the volume of the can, we just go back to the formula for the volume of a cylinder, plug in our found radius and height, and compute!

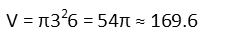
The can must necessarily have a volume of 54π cubic units for all of our conditions to be met. Nothing else will work.

We solved this problem by merely recognizing the relationships as stated in the set-up. Using those, we were able to draft equations from the known formula for our objects, and using a little bit of algebra, find the unknown radius and height. So just because you don’t see any numbers in a word problem, don’t take that to automatically mean you don’t have enough information to solve it. If you examine the constraints carefully, you just might!