Math Made Easy: Problem of the Day 122

Whenever we can, diagram. So often, a picture can help solve the problem by allowing us to take advantage of the human capacity for visual thinking. It’s just part of our biology that we’re visual creatures, so whenever we can make something concrete and visible, we should.

Our initial diagram of the situation should look something like this. We mark the angles of elevation (basically, how much they have to lift their eyes to look at the rocket), and the height of the rocket. Since Anja has a steeper angle of elevation, we can reason that she’s probably closer to the launchpad than Mike. We also recognize that the triangles we draw with the lines from their eyes to the rocket and the rocket to the ground are right triangles, which really does make the problem much easier. We only have two triangles to solve – find their bases, add them, and we have our answer.

We're also going to make a couple assumptions here. First, we're going to ignore the curvature of the Earth. At these distances, we may as well consider the Earth flat, for it is huge, and we are small. Second, we're going to assume the rocket went straight up - or at least stayed directly in between Mike and Anja. Without this second assumption, we actually need a lot more information than we have, and the problem becomes much, much more difficult.

If Mike’s angle of elevation is 45°, then his right triangle must also be isosceles – the height and the base must be the same. So we know that he’s 3km away from the launchpad. Let’s label our diagram with that figure. We will also call Anja’s distance from the launchpad x.

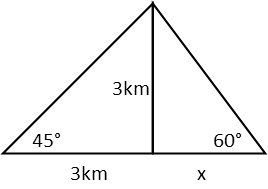
We can readily find x by using the tangent function – it’s the opposite side over the adjacent side. We don’t have the hypotenuse for her triangle (though we could easily find it using the sine function OR by recognizing this is a 30/60/90 triangle and using a little bit of multiplication), but we don’t need to do so. Let’s just go straight to the base using the tangent.

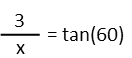
With our equation, we need to solve for x. Since x is on the bottom, and we don’t want it there, we can simply swap it with the stuff on the right-hand side of the equation. It’s kindof like cross multiplying, but more like taking the two steps of taking the reciprocal of both sides of the equation than multiplying both sides by three all as one step. That puts us in the form where we can just compute, and we do so, finding x to be the square root of three. So she’s about 1.7km away from the launchpad.

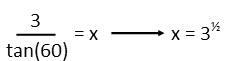
Having found Anja’s distance from the pad, we now just add their distances, and, voila, we’re done – we know the two are about 4.7km apart from each other.

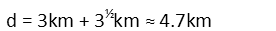
Remember that a picture can almost always help you see your way to the solution of a problem. Even if you’re confident you know the math behind it, still draw that picture. It’ll confirm your math, and might also help you see an even easier way to your solution than your initial plan.