Math Made Easy: Problem of the Day 123

One of the great disservices in our education system is a failure to teach students early on what an operator actually is. Heck, we don’t even call them operators when talking to most elementary students, but instead call them “symbols.” We refer to operations when we’re teaching, but not really saying “this symbol is the operator, and it tells us to do this.” By calling them just “symbols” we end up confusing our students. They end up treating each operator as a separate thing rather than a group of objects that each tell us to do something slightly different. So when they encounter a new operator, they have no idea where to begin – they don’t know that they’re now being told to perform some new operation with the numbers (or variables) at hand. This can cause them to come to a complete screeching halt and just stare at the paper, rather than trying to figure out “Okay, what does this operator do. What sort of manipulation am I supposed to be doing now.”

And standardized tests LOVE to take advantage of that by throwing out new crazy-looking operators to see what kind of mental lock it imposes on the student. And that’s really all this problem is about – there’s a crazy new operator. Here I use the Latin closed lower-case omega, but we can call it moog. All it tells us is: “take these things to the left and right of me, and do this set of manipulations with them.” So everywhere we see moog, we take it, the thing to the left, the thing to the right, and replace them with the definition of moog, where the thing to the left goes where the a’s are, and the thing to the right goes where the b’s are in that definition. When we do that, we should get something that looks like this:

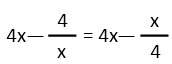
Now we have an equation that looks a bit more familiar. The crazy operator is gone, and it looks like something we can do algebra with. The first thing I notice, is that there’s a 4x on both sides of the equation, so we can just cancel both of those out straight-away.

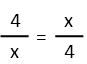
Now we’ve got a proportion of ratios. Normally I advise against cross-multiplying, but here is one of the few circumstances where I recommend it, because in this case it really is the next step that will most quickly get us heading towards our answer. So we multiply the x’s and the 4s:

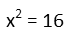
And all we have to do now is take the square root of both sides to undo the square. Remember that whenever we take an even root, we must have two answers – a positive, and a negative. So we use the plus/minus operator to denote that the number to the right of it can be positive or negative.

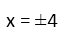
It turned out this problem is actually incredibly easy. Just don’t let strange new operators throw you for a loop. Rather than sitting there staring at them going “what the heck,” just look for their definition, and replace them, and the stuff that goes with them, with that definition. It’ll make your life a lot easier. It’ll also get you ready for many of the crazy new operators you can run into in higher math and physics – especially quantum mechanics where our mathematics practically takes on a new language of its own.