Math Made Easy: Problem of the Day 124

Physics! Among the many uses of mathematics is the ability to manipulate equations to predict how the physical world around us will behave. This helps us master our environment and build nifty machines that do incredible things. Machines we absolutely would not be able to construct without math. Combustion engines work on thermodynamic principles. Heat is added, and a gas expands, moving a piston which then moves other things. In a real engine, the gas expands explosively, which makes the equations much more complex, but for our purposes, we’re going to consider a gas expanding smoothly and behaving by simple rules.

We first recognize, that since the chamber of the piston is at equilibrium with the surrounding atmosphere, that the piston is at rest and the gas in the chamber is at the same pressure as the atmosphere. We will also ignore friction in the cylinder and consider the piston itself to be essentially massless so that it moves completely freely.

With our conditions and assumptions set, we’re ready to begin. When gases are heated, they expand. This is because the molecules are already zipping about, and when thermal energy is added (heating), they move even faster, zipping about more, covering more ground. So they must either expand or exert more pressure on the walls of whatever container is holding them (in the form of crashing into those walls). Since our piston moves freely, so the gas will push against the piston and move it, maintaining pressure equilibrium with the atmosphere. So this tells us that of the four things that *could* change: pressure of the gas, volume, amount of the gas, and temperature, that only two things are changing in our situation: the temperature, and the volume. We can use the ideal gas law to determine just how the volume will change when we increase the temperature. Let’s remind ourselves of what it looks like:

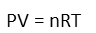
Now write it recognizing the things that are changing by denoting those things with a δ:

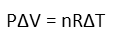
And we move the Pressure variable to the right-hand side by division so that our change in volume is isolated.

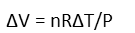
We remind ourselves of R, the Universal Gas Constant, in units that will be useful for our problem (here, we want Liters, atmospheres, Moles, and degrees Kelvin).

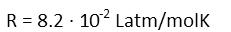
And we plug in all our numbers to find the change in volume.

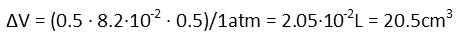
Now here’s a beautiful thing. We *could* find the original volume of the chamber at this point in time, add in the change in volume, then calculate the change in the height of the cylinder. We only know that only the height is changing since the piston is the only thing moving – the walls remain in place, so the radius of the cylinder is a constant. BUT. We don’t actually need to know the original volume of the cylinder. Now that we have the change in volume, all we have to do is divide that by the base-area of the cylinder – in other words, divide it by πr².

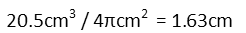
We *could* calculate the original volume of the cylinder, add in the change to that volume, and then calculate the resulting change in cylinder heights. We’ll find we get the same thing (go ahead and do it for some extra practice). But since there’s a faster way to do it, we needn’t bother. And trust me, physicists don’t do extra math when we don’t need to do so. We do enough of it as it is.