Math Made Easy: Problem of the Day 125

When dealing with collisions, one first must consider what type of collision it is. Is the collision elastic, where the two objects bounce away from each other like crazy balls? Or is it an inelastic collision where they at least partially stick together and continue moving as one? This is important to determine, as, in the case of elastic collisions, kinetic energy is conserved, while for inelastic collisions, kinetic energy is lost in some form, usually to heat.

For today’s instance, we are clearly dealing with an inelastic collision – auto accidents always involve a loss of kinetic energy as the vehicles crumple, and in this case, they even lock together. So we know that the kinetic energy of the system before the collision does not equal the kinetic energy of the system after the crash. But how do we determine the amount of energy lost? Is there a simple formula for that? Well, there is, but if we tried to remember every formula in the universe we’d be playing the role of Sisyphus trying to roll the boulder up the hill. So let’s derive it ourselves.

We do know that, regardless of whether kinetic energy is conserved in a collision, momentum must ALWAYS be conserved. There aren’t different types of momenta like there are energy, so it doesn’t have anywhere to go but in a different direction. So we shall start by examining the system’s total momentum before and after the crash.

The car is at rest, so it has zero momentum to start. The truck, however, is moving. We don’t know how fast, but let’s not let that get in the way. We can do all our algebra in variables and see later whether or not the truck’s unknown velocity is going to be an issue. We’ll call the truck m₁ and the car m₂. Our equation for the truck’s momentum (and therefor the system’s total momentum) before the collision is:

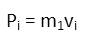
Afterwards, the two vehicles are stuck together, so we have essentially the same momentum equation, only the mass is now the total mass of the vehicles, and the velocity is now another unknown velocity:

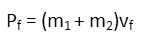
We set the two momenta equal two each other, plug in the right-hand sides for the before and after. And while we’re at it, I have an inkling I might want to relate one velocity in terms of the other, so I’ll relate the final velocity in terms of the initial velocity and the masses. This will help later on to reduce our unknown variables to only one.

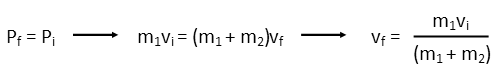
Now for our kinetic energies. Again, since the car is at rest before the collision, it has zero kinetic energy. Therefor the system’s total kinetic energy is just that of the truck:

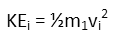
Afterwards, the kinetic energy involves the sum of their masses and the final velocity:

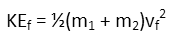
To find the portion of kinetic energy loss, we take the difference of the kinetic energy before and after, and divide it by the kinetic energy before the collision:

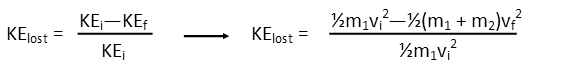
We can factor out that ½ and get rid of it.

Now let’s make the substitution for the final velocity in the terms we found for it in our momentum equations. This’ll leave us with just one unknown variable, the initial velocity, since we know both masses. While not ideal, it still is much better than having two unknown variables. Whenever you can reduce your number of unknowns, legitimately, do so. And, interestingly, though the equation gets a bit uglier when we make that substitution, we see that we can get rid of a factor in the new fraction we added up top. That (m₁+m₂) parenthetical cancels one in that top fraction's denominator, getting rid of the square. That cleans it up a little right away.

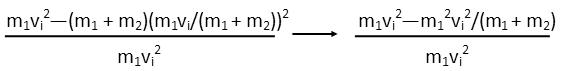
Now I see that there is a common m₁v_i factor in all three terms. That cancels and goes away. This is looking cleaner by the moment. And since everything is over 1 after that cancellation, we no longer have a fraction in a fraction, which is happy.

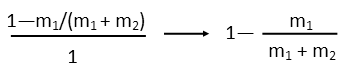
But we do want to make this as simple as possible, so let’s give the 1 and the fraction a common denominator so we can combine them back into one fraction.

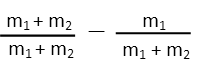
When we do that, we see the m₁ terms in the numerator cancel each other right out, leaving us with only one term in the numerator. Nice! What looked like a complete mess for a while has actually turned into a very nice, neat little formula for the portion of kinetic energy lost, and entirely in the only variables we know. We didn’t need those velocities after all, which is great, and also tells us something fundamental about the physics involved – at non-relativistic speeds (velocities so slow we don't have to worry about relativity), when two objects collide inelastically, the kinetic energy lost is dependent solely on the relative mass of the objects involved. Let’s plug in our numbers now and find out just how much energy is lost.

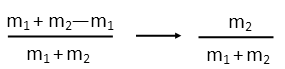
So one-sixth of the system’s total kinetic energy is converted into something else, most likely heat energy.

This problem is a great example of just why you want to do your algebra BEFORE you start plugging numbers in. If we’d just started trying to put in numbers, we might have gotten to that unknown velocity and come to a screeching halt, wondering what the heck we’re going to do now since we didn’t know it. By just doing our algebra first, we managed to eliminate those unknown variables and arrive at a very simple, easy to manipulate expression. Keep that in mind.