Math Made Easy: Problem of the Day 126

Usually when you see a question like this one on a standardized test, they’ll provide a little picture. Regardless of whether they do or not, make your own. Don’t trust theirs. Frequently they’ll draw it off-scale on purpose to attempt to deceive you. The SAT especially is fond of drawing pictures out of scale. Graphing this situation, we get the picture below.

Note I’ve already included the altitude to IN. The altitude to any side of a triangle is that line which is perpendicular to that side and intersects the opposing vertex. The fact that the altitude is perpendicular is what is going to make this problem readily conquerable. Since it is at a right angle to side IN, let’s find the slope of IN first. Reminding ourselves of the formula for finding the slope of a line given two points on that line:

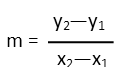
Remember, the y’s go on top and the x’s on bottom. Or another way to keep it straight, up-and-down on top, left-to-right on bottom.

I will pick Point I as Point 2 and Point N as Point 1. Plugging those in we find the slope of IN.

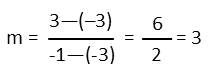
Now here’s where we get to take a short cut. To find a line perpendicular to any given line, we just take the original line’s slope, make it negative, and take the reciprocal – or just flip the fraction and make it negative. All lines with that slope will be perpendicular to the original line. But we want one specific line. Don’t we need to find the full equation of line IN? The beauty here is, we don’t. Any line equation we find with the negative reciprocal of 3, or -⅓ will be at a right angle to IN. The only line that’ll work for us, however, MUST pass through point W. So to find that line, we can bypass finishing the equation of IN and go straight to finding the equation of our altitude. Let’s use the point-slope form of a line to find it.

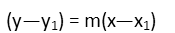
So we insert our slope of -⅓ and the coordinates of point W. I’ll also go right ahead and distribute that slope on the right-hand side.

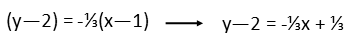
To finish, we just add 2 to both sides to get the equation looking like slope intercept form, which reads y = mx + b.

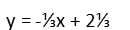
And we’ve found our altitude equation. We’re done. If you like, go ahead and finish finding the equation for line IN and graph both the lines to prove to yourself that they are indeed at right angles.