Math Made Easy: Problem of the Day 128

Here’s another problem with multiple ways to do it. I’ll address two of them, both of which are fairly close in difficulty and speed. But for both, we’re still dealing with a circle. And whenever you’re dealing with circles, you almost always want to know the radius of the circles involved. So it’s frequently a good idea to start there, especially if you’re not sure of what strategy you want to use to tackle the problem.

To find our circle’s radius we remind ourselves of the formula of the circumference of a circle, and we readily see that r MUST be 1.

For both methods, we draw a diagram, since you always want to do so for any problem where you can. Using as many parts of your brain as you can is just the smart thing to do, and nothing helps trigger your visual cortex like a picture. Note that in the picture below I already filled in a lot of the numbers we’ll calculate in a moment.

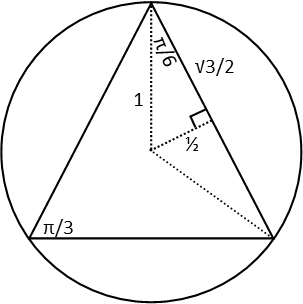
For the first method, we break up the triangle into smaller triangles. We do this so that we can find a right triangles that might make solving the larger triangle easier. We first draw a line from one of the vertices of that triangle to the center of the circle. That line is the radius, so it has a length of 1cm. From there, we draw another line perpendicular to one of the sides of the equilateral triangle. This forms a right triangle. Note I also drew a radius to one of the other vertices just to help recognize that there will be six of these small right triangles.

Now that we have right triangles, we can start examining our layout. An equilateral triangle is also equiangular. This means all three angles are π/3 radians in measure. (I’m sticking in radians to make things easier – it usually is). The radius of the circle drawn from the vertex of the equilateral triangle necessarily bisects the angle. That means, for the right triangle, that angle is π/6 radians, and the hypotenuse of the right triangle is 1. If that angle formed by the bisection is π/6 radians, then the right triangle must be a 30-60-90 right triangle (I named it here in degrees to make it more recognizable). That’s fabulous.

It’s fabulous because there are two special kinds of right triangles: the 30-60-90, and the 45-45-90. They’re special because we can remember three numbers for them that are the same three numbers one should remember to build a unit circle (which is what our circle here is, by the way!):

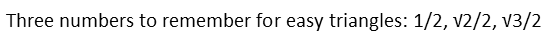
I wrote those numbers in order of bigness on purpose. It helps remember which goes where. Each number represents the length of the side opposite the appropriate angle for the special triangles, when those triangles have a hypotenuse of 1 (which ours does). The small number goes to the side opposite the small angle. The medium opposite the medium angle. And the large opposite the large. So that means ½ goes with 30 degrees (or π/6 radians), √2/2 goes with 45 degrees (or π/4 radians), and √3/2 goes with 60 degrees (or π/3 radians). If your triangle’s hypotenuse is bigger than 1, you just multiply those numbers by whatever the hypotenuse is. I wrote the multiplication out here, even though our hypotenuse is 1, just to demonstrate.

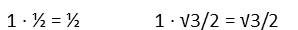
So with all 3 sides of our small right triangles known, we remind ourselves of the formula for the area of a triangle where we know its height.

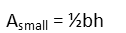
We recognize again that the equilateral triangle is made up of six of those small right triangles, so we just multiply the area of one of them times 6:

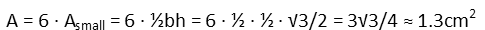
And we’re done via that method. The inscribed equilateral triangle has an area of about 1.3cm². Now let’s try another method and see if we get the same answer. We better, or we did something wrong with one of our methods (or both!).

We can actually go directly to the area of the triangle without calculating any of its sides, or any of the component triangles. We do this by area subtraction. We know a formula for the area of a circle, and the area of an arc segment (part of a circle cut off by a cord). The sides of the triangle make the chords that will make each arc segment. We see that, but area subtraction, if we take the area of those three arc segments away from the area of the circle, we’ll have the area of the equilateral triangle.

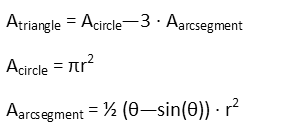
Now, that θ in the formula for the area of the arc segment is for the angle of the central angle that describes the arc involved. We don’t have that central angle – we have the inscribed angle that describes each arc in question. Or do we? There is a direct relationship between a central and inscribed angle that describe the same arc. Since the central angle bears the same measure as the arc, and the arc has twice the measure of the inscribed angle that also describes it, we can reason that the central angle also has twice the measure of the inscribed angle. So when we plug everything into our formula, we actually *can* use that inscribed angle – we just have to multiply it by two everywhere it shows up. Also not that the formula for the area of an arc segment is in radians – if you plug the measure in degrees into that form, you will be very, very wrong. That’s why I stayed in radians for this problem. So, let’s plug everything in and see what we get.

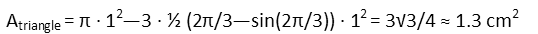
Voila! We got *exactly* the same answer, which is what we should have gotten. Outstanding! Anything else would have served as an error check telling us we need to go back and look over our math to find either the error in our computation or our reasoning.

Can you find another method?

And, for an added challenge, what would the area of the triangle be if the circle were inscribed in it, and not the other way around?