Math Made Easy: Problem of the Day 129

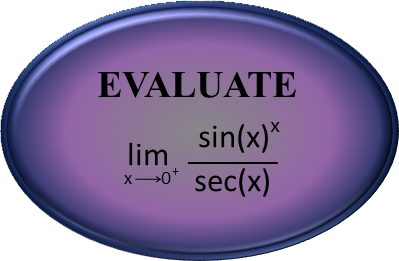
Understanding limits is fundamental to conquering calculus. The fundamental theorem of calculus is based on limits, and many problems (especially improper integrals) are solved using limits. So it’s good to be able to handle them, and understand how to navigate tricky ones.

The limit of a function or expression is the value of that expression, or the value it most closely approaches, at a given point. Since the function may not exist at some points, this can be difficult to assess at times. In some cases, it doesn’t exist at all. How we know whether or not the limit exists, is we examine the function coming from the left and from the right. If the limits exists on both sides, AND IS THE SAME on both sides, then the overall limit of the function exists. That means that both sides are approaching the same thing, even if they never reach it.

The first thing we always do when checking for limits is plug in the number for the location of the limit we’re seeking. Here, we’re wanting to know what the limit of the function is as x approaches zero. So we plug in 0 everywhere we see an x and see what we get.

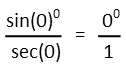
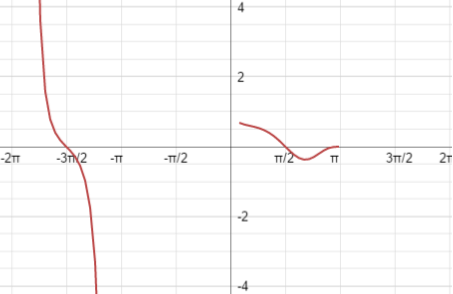
Well, that doesn’t look very good, now does it. We get 0⁰ up top, which means 0/0, which is undefined. We can’t divide something into no parts. That makes absolutely no sense whatsoever. So let’s look at the limit coming from both sides. Coming from the right, our function approaches zero, but ceases to exist as it gets close. It’s positive as it approaches. Coming from the left, it ceases to exist as a real number far from zero – but it becomes infinitely negative before it does so. There’s an entire area where the function is imaginary. This means no overall limit exists. But we can still examine the limit from the right-hand side, as our problem requests. If we were just looking for an overall limit, we’d be done right now.

But what do you do when you plug in those numbers and get something undefined? Well, this is where something called L’Hôpital’s Rule comes in. It’s very handy for solving these situations, and ONLY works for situations where we get something undefined – 0⁰, zero divided by zero, infinity divided by infinity, or so on. L’Hôpital’s Rule tells us that when we have one function divided by another function, we can find their limit by looking for the limit of the top one’s derivative over the bottom one’s derivative. In other words, just take their derivatives separately, and leave them as a fraction, then see if you can find a limit. It looks like this:

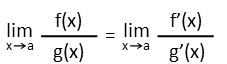
For our problem, I’m going to ignore the sec(x) on the bottom, since it comes out 1 when we plug in zero for x. It’s not our problem. The top is. But to use L’Hôpital’s Rule, we need the top to look like a fraction. So how do we do that? We’re going to do a couple tricks. First, we’re going to take advantage of logarithms to get rid of the power of x. I’ll pick the natural log for a very specific reason involving its derivative.

We write our top as an equation of y in terms of x, careful to keep the limit in there.

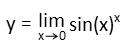
We then take the natural log of both sides.

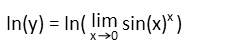
A property of limits allows us to bring the natural log on the right-hand side inside the limit.

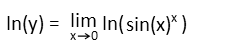
With the natural log outside the limit, the exponent property of logarithms allows us to take that exponent inside the log and bring it outside as a coefficient.

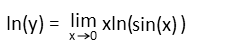
Now here’s where we’re going to get a little sneaky. We’re going to rewrite that coefficient x giving it a negative exponent. In order to avoid changing the value of our expression, we need to turn the expression into a fraction, putting that coefficient x on the bottom as we do so. Remember that a negative exponent just means put the base with a positive exponent on the bottom of a fraction. So a negative exponent in the denominator is the same as that thing with a positive exponent in the numerator, or as a coefficient.

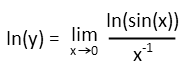
So now that we have our limit in terms of a fraction, we can apply L’Hôpital’s Rule. Since it lets use take the derivatives of the top and bottom separately, we don’t have to deal with the Quotient Rule of Derivatives. But up top, we do need to use the Chain Rule. Which really just tells us to do this:

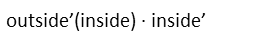
Which means take the derivative of the outside function, leaving the stuff inside alone. Multiply that by the derivative of the inside function. Applying that to the top of our fraction, we see that the derivative of a natural log is 1 over the thing inside the log. So our derivative of the top is one over the sin(x) times the derivative of sin(x), which is just cos(x). Our derivative up top looks like this:

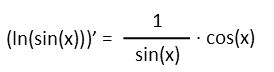
The derivative down below is easy. We just follow the power rule of derivatives.

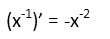
Putting them together, and recognizing that 1/sin times the cos is the same as cos/sin, which is the cotangent. The cotangent is the reciprocal of the tangent. We also have a reciprocal in the denominator (since that’s all a negative exponent is). So let’s just flip everything. But when we do that, and plug 0 in to find the limit, we get an undefined answer again. Drat!

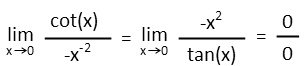
Don’t worry, though, because the beauty of L’Hôpital’s Rule is that we can do it over and over and over again until we finally get something that is not undefined (unless we see a pattern where we’re never going to get that). So let’s do it again, taking the derivatives of the top and bottom, plugging them in, and substituting zero for x.

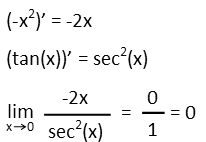
Well, we got something defined this time. BUT, we’re not done yet. While we found a limit, we didn’t find the one for which we’re looking. Remember that when we started our steps to be able to apply L’Hôpital’s Rule, we wrote an equation for y in terms of x. And as part of our process, we took the natural log of BOTH SIDES. That means what we just found was the natural log of y, not y itself. So we set ln(y) equal to zero, and see that y = 1.

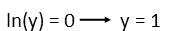
Also remember we ignored the denominator of our original limit function to do all this. Let’s remember it again. So we get 1/1. Our final limit is 1.

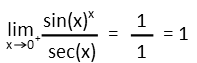
L’Hôpital’s Rule is a very, very useful tool in calculus. It can make seemingly impossible problems fairly easy. But also remember that, along the way, you might change your problem so that the answer given by L’Hôpital’s Rule isn’t quite the answer you want. So don’t just get one limit, and say, “I’m done,” and move on before asking yourself what you really calculated. If we’d done that here, we would have been wrong.