Math Made Easy: Problem of the Day 13

Time for some relativity. One of the interesting consequences of physical laws being invariant regardless of one’s frame of reference, is that time, velocity, and distance all become relative – they are observer-dependent. For instance, on a train, to your point of view, the world around you is sliding past. But to an observer on the ground, it is you who are moving. For today, let’s address a relativistic problem.

A rocket is travelling between two space stations. Those stations are 100,000,000 kilometers apart, or about twice the distance from Earth to Mars. It takes the rocket one hour to make the trip, according to station controllers (it's a superfast rocket, beyond today's technologies). How long did the trip take to passengers on the rocket? Was it less time or more time than the station controllers recorded?

To determine this, we need to use Lorentz Transformations – equations that allow us to transform time, distance, and velocities between two different moving frames of reference. The apostrophes just mean “prime” which is just a way to denote one frame of reference from another. So everything marked without a prime is in one frame of reference, everything with the prime in the other. Note that the only thing that doesn’t get a prime is c, the speed of light, and that’s because it’s the one thing that DOESN’T change depending on relative motion – it’s invariant, and that’s because of light’s role as the information carrier of the universe. The two equations we might need for this are:

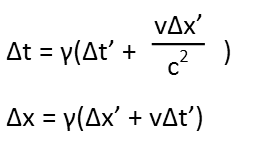
Note that they’re the same regardless of our frame of reference. If we want to convert from prime to non, then we just switch the prime symbols, and the plus to a minus (if we’re converting from the frame we know the velocity in to the other frame). Also note that γ is found with this equation:

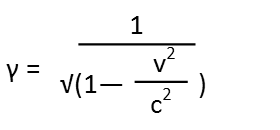
Now that we have those, we can answer our question.

How long did their trip actually take according to the passengers? Note that Δx is just the distance travelled, or how far apart our two stations are. We’re also going to convert our units for consistency. 100,000,000km are 10¹¹ meters, and 1 hour is 3,600 seconds, or 3.6x10³ seconds. We first need to calculate the rocket’s velocity relative to the space stations. After a quick calculation, we see it’s going 2.8x10⁷ m/s, which is a significant fraction of the speed of light. That thing is moving – almost 1/10^th the speed of light!

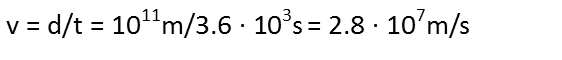
Next, we need to calculate our γ. Plugging in our units as we go, as we should, we see they all cancel out and gamma is unitless. This is good, since it’s supposed to be – it’s just a correction coefficient.

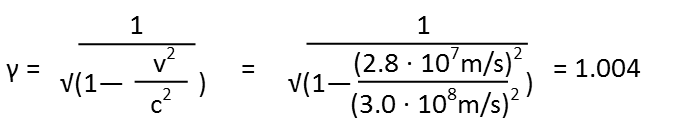
Now we plug everything into our time transformation, noting our units, and seeing that they cancel out to seconds, which is what they should do. We use the transformation where we subtract since our known velocity is that of the rocket perceived by the station controllers and not that perceived by the passengers:

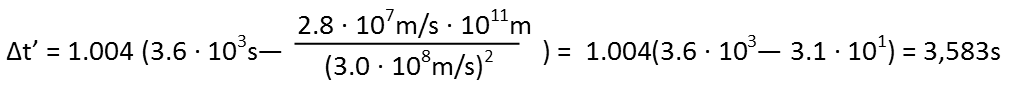
We could convert back to hours, but we don’t really need to do so. To our passengers, it took them 17 seconds less to get there than the station controllers recorded. This stands to reason - the closer to the speed of light you go, the most slowly time appears to move to you than to the outside universe.

If you’d like to do the calculations (remember you'll need a new gamma), you’ll find that if the stations were ten times further apart, and the rocket covered the distance in the same time (one hour station time), the passengers would experience only 22 minutes and 41 seconds of travel time. But then, the rocket would have been 93% the speed of light to do so, which, under our current technology, would require more energy than we could possibly fuel.