Math Made Easy: Problem of the Day 130

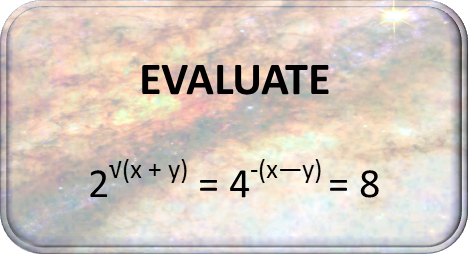
When we’re asked to evaluate things, we always need to ask ourselves some basics about what’s going on. Here, we have two main things happening. We’ve got a system of equations (though it’s written to pretend it’s one equation), and we’ve got exponential equations. With two equals signs, we’ve basically got three equations.

Let’s break it out to show that it really is three equations. When we do so, it should look something like this:

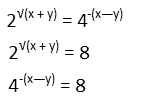
With that, we now recognize that we’re dealing with exponential equations. And when we do, we usually want to find a common base for everything, if we can. 2, 4, and 8 can all be written as powers of 2, so we can give everything a common base of 2. All we have to do is multiply the 4 exponent by 2, and write the 8 as 2³. Like so:

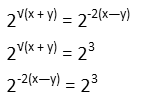
Now that everything has a common base, we can ignore that base. Yup, ignore it. Just write everything again as if it’s not even there.

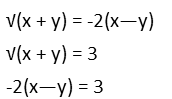
We now have what looks like a set of mostly linear equations, except for that square root. If we square everything, we can get rid of the root. And maybe make the system a bit easier to deal with. For this system, I’m going to leave everything in factored form on purpose.

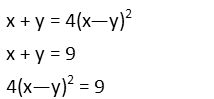
I left the quadratic factored so that I could actually find its roots. We’ll do that by dividing both sides by four, and then taking the square root of both sides. This gives me ±3/2. But I need to be careful with those roots. That square root in our original equation? It limits the domain for our system. Since the square root can’t produce a negative number, we know that -2(x – y) must be positive. And positive 3/2 won’t do that – that’ll make -3 when multiplied by -2. The only thing we can multiply -2 by to get positive 3 is -3/2. So we know that’s the root we want from this quadratic.

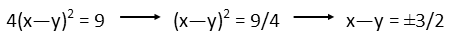
Why’d I do find the root of the quadratic, you ask? Well, because, in their current forms, we cannot solve this system of equations by elimination. We could try substitution, but the method I’m using is actually easier. By finding the root of the quadratic, and recognizing that, since it’s a square, they’re both the same, I can use it and that middle equation in the system to solve by elimination. I’ll do that now. When you solve by elimination, be careful to line your two equations up nicely so you don’t make mistakes. For our equations, it’s convenient that the y’s have opposite signs, and that everything has the same coefficient. All we have to do is add the two equations, and the y terms go away. But before I add, let’s at least give the constants a common denominator to make our lives easier.

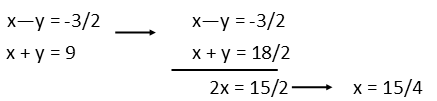
We found x for our system. Now all we have to do, is pick one of the equations, plug it in, and solve for y. It’s our pick of the equations, so always choose the one that looks to you to be the easiest one to solve.

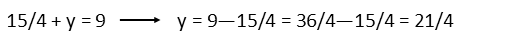
And there’s our y term. Since the system is largely linear (just with a square root in it), we know that there should only be one solution, so we’re done. Go ahead and test the solution pair – it’s a good idea to do so when you think you’re done with your problem. Use the original equations to test – that’ll help you make sure you didn’t make and sign errors or domain errors.