Math Made Easy: Problem of the Day 130

Let me start this article by saying, if you don’t know what you’re doing, trying to build your own taser is a BAD IDEA. That said, as we’ll discover, it’s a good thing Tom only has a 9V battery, because he’s not going to be able to do much damage to himself or others while trying to build his ill-conceived contraption.

So let’s make a few assumptions while we do this. First, his design will actually work. Second, he can seal the tube well enough that the vacuum is retained. And third, that the capacitor he builds is able to deliver all its energy in one jolt. Those made, we can continue with the math.

A taser is essentially a large-ish capacitor on a high voltage circuit. Capacitors are devices similar to batteries –they store energy in the form of an electrical charge. The primary difference between capacitors and batteries is one of discharge time. A battery will release its energy only slowly, while a capacitor is generally only limited by the circuit its own for the speed of its discharge. We use them when we need that energy delivered in quick bursts, like in a flash bulb or for tasers. The capacitor takes advantage of the resistance of the material a gap between two metal plates to allow a voltage to build up with all the charge on one plate. The maximum storage of the capacitor is the point at which there are so many charges on that one plate that they can leap across the gap onto the other plate, regardless of the voltage on the circuit (or, in some cases, the force induced by the charge difference becomes so great that the plates are literally pulled together – I’ve accidentally done this with my capacitors a couple times).

We can easily calculate the amount of energy a capacitor can store. We use the following formula to do so:

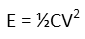
Here, C is the capacitance, which is a geometrical property of the capacitor, and V is the voltage applied to the plates – which in our case will be that applied by the battery. To calculate the capacitance is easy, since it’s based solely on the geometry of the plates. We can use the following formula to do that:

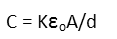
In the capacitance formula, K is the dielectric constant of the material. For vacuum, that’s 1. ε₀ is a constant representing the permittivity of free space (permittivity is basically a material’s capability to store electrical energy). A is the cross-sectional area of the plates of the capacitor, and d is their distance apart from each other. We like to measure these in meters, so make sure you convert your units accordingly. The permittivity of free space is (note that C here is the unit Coulombs and not a variable):

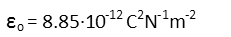
Let’s plug the capacitance formula in for C in the energy formula.

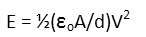
And now we just plug in all our numbers to find out how much energy the capacitor stores, and thus has available for discharge. Now, when we plug in our units with our numbers, it may not be obvious that they cancel properly to get Joules. But recognize that a Volt is the same a J/C, so the Couloumbs cancel there giving us J². And a Newton can be written as a J/m. Since that’s a reciprocal, that flips, cancelling one of the Joules left over, and all the meters cancel each other. So we’re nicely left with just Joules for our units, which is what we want.

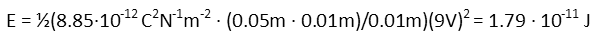
Well, that’s not very much, now is it? Tom made a couple mistakes building his capacitor. First, he only used a 9V battery to charge his capacitor – since the voltage applied is very important for the energy the capacitor stores, that small a voltage isn’t going to cause the taser to hold much energy at all. Second, he used a vacuum tube. Since vacuum can’t really store much electrical energy, he’d have been better off using something else to separate the two plates. Just what, I won’t say. I purposefully made his design useless. This was just for the purposes of illustrating the math behind the capacitor, after all.