Math Made Easy: Problem of the Day 133

Definite integrals are incredibly useful. We can use them to quickly compute volumes and other large sums that might not be easily done without calculus. But they’re backwards to the way we think. Just like division is generally harder for most people than multiplication, integral are a trickier task for the majority of folk than the derivative, of which they are just the reverse function. So how do we conquer them?

When we approach them, we need to always keep in mind that they’re just backwards derivatives. So we need to take our familiarity with the derivative in mind. When we look at that integral, does it look like something we’ve done before, in reverse? Have any of our differentiation problems ended up with something looking like this? Even when it may not be readily evident, they probably have.

In this case, I see a 1 over some junk. Whenever I see that, I immediately think logarithms. Why? Well, because the derivative of log(x) is just 1/x. So that’s going to be part of our original function (I like to think of the function we’re looking for when we’re integrating as the original function, since we’re working backwards). But there are two parts to our integrand – there’s also a log(x) in the bottom. Well, the fact that those two parts are multiplied gives me a clue as to what’s going on. I’m going to assume that there is something going on with the chain rule of derivatives – whenever you have one function inside another, you end up with the derivative of one times the derivative of the other. Or, as a reminder, it looks like this:

Our integrand looks very similar to that, only as a reciprocal. And since I know the derivatives of logarithms end up as reciprocals, I can reason that the integrand is the derivative of log(log(x)). One function inside another. And it works.

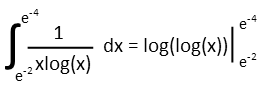
So now we need to evaluate our result. The e terms on the top and bottom of the integral operator tell us to evaluate our integral by plugging those numbers into our results. We first plug in the top one, then we plug in the bottom one, and subtract the results of the top from the results of the bottom.

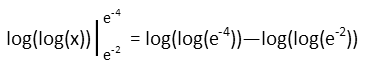
Well, isn’t it convenient that the numbers we’re evaluating are powers of e? Any log of e^x is just x. So, working from inside to outside, we recognize that. Then we see that subtracting one logarithm from another allows us to invoke the quotient property of logarithms in reverse so that we can combine them, giving us a fraction inside one logarithm. And then we can simplify that.

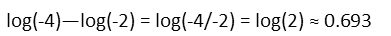
So our result is just log(2), or about 0.693.

Just remember when you’re integrating you’re working a derivative backwards and try to think of it in terms of “what derivative gives me this?” Remember the rules of derivatives, and some basic derivative types, and you’ll be able to solve them in a pinch.