Math Made Easy: Problem of the Day 134

Many three dimensional shapes can be defined by expressing their outer surfaces as curves wrapped around the axis of the object. The volume of these objects cannot be found by simple geometric methods. Since the curves can define changing radii, one would have to imagine infinitely thin slices through the object, find the area of those slices, and then add them all up. That is the very definition of the integral – a sum of infinitely thin slices. So to find the volume of our object, we must find an integral of the curves.

But which integral? Let us first look at the curves. We can graph both of them, before rotation around the y-axis. They look like this:

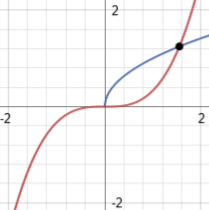
Note how the curves intersect in two places. That area in between the two curves will form the shell of a bowl when we wrap them around the y-axis, like this:

So now let’s consider those infinitely thin slices again. We can note that, for each slice, the area of the shell will be a ring defined by the radius of the outer curve minus the area of the inner curve. But we need to change the form of our equations to get the area of this ring. If we leave them in terms of x, we won’t define a ring, but rather flower petals formed by infinitely thing vertical slices. We want horizontal slices, since our axis of rotation is the y-axis. If we were rotating around the x-axis, we’d keep the integral in terms of x. We therefor need to rewrite our equations in terms of y rather than x.

Now we need to express the cross-sectional area of each slice in terms of the varying width of the rings:

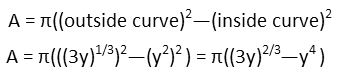
With that cross-sectional area defined, we can now recognize that volume is the integral of area. So we place the area equation inside the indefinite integral.

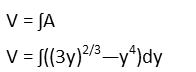
Before we continue, we need the limits of integration. An integral exists over the entire domain of the integrand (the expression inside the integral). But we don’t want the entire domain since one of our curves exists over all real numbers and the other exists from zero to infinity. We only want the area where the curves intersect. That means we need to define our limits of integration from the first point of intersection to the second. We can find those points by setting the equations equal to each other and solving.

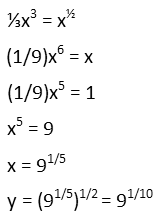
Note that I only showed one solution there. It’s also evident from the initial set-up of the equality that zero is a solution, and our graph supports that. So our limits of integration are from 0 to 9^1/10.

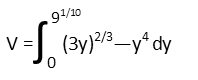
We work our integral recognizing that it’s just a backwards derivative. That means that, for each term, we increase those fractional exponents by 1 and multiply the term by the reciprocal of the new coefficient. It’s fortunate that each term is the result of only a single function – we don’t have to worry about thinking of the chain, product, or quotient rules of derivatives at all. These were simple integrals, even if the fractional exponents made them look otherwise.

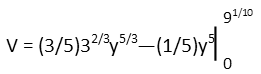
With the result of our integral, we just need to evaluate. So we plug in the upper limit to our result, and then subtract from that the same result with the lower limit inserted. Conveniently, the lower limit being zero makes that part of our evaluation go away.

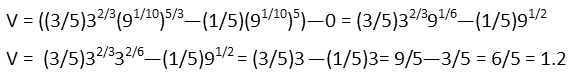
We’ve found the volume of our bowl-shaped solid: 1.2 cubic units. The key to getting this correct was remembering that we had to change the form of our equations to terms of y. The tendency of many people would have been to do one of two things (or both): Leave the equations in terms of x, which would have given us a different volume, or to use the limits of integration as the x-coordinates of those two points of intersection instead of the y-coordinates, which would have given an incorrect volume. So make sure you pay attention to the correct axis of rotation, and don’t do all that work for nothing.