Math Made Easy: Problem of the Day 135

Even when we know all our rules and processes for doing math, sometimes we’ll be faced by a problem where we really don’t want to work every single step to get to the end just due to the sheer amount of work it’ll take. If we can figure out a way to eliminate steps or to see a pattern and reach a reasonable conclusion, we should take it.

Whenever you see the n^th derivative of something, you’re being asked to find that expression’s derivative. Then take the derivative of that result, and keep taking the derivative of the new result until you’ve done that n times. But do we REALLY want to do 100 derivatives in a row to come to our answer? Not really, not if we can find a better way to reach our conclusion. Perhaps if we take a few derivatives, we might see a pattern, and from that pattern, draw a conclusion as to what the 100th derivative of our expression might be.

First, let’s rewrite the expression. I’m a big proponent of always finding a way to write division problems as multiplication when you can. Here, we just change the sign of the exponent in the denominator. That has the effect of bringing it out of the denominator to make the problem a multiplication problem.

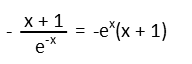
Now that we were able to do that, let’s remind ourselves of how the product rule of derivatives works:

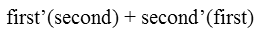
And now we apply it, multiplying the derivative of the first term by the second term untouched and adding that to the derivative of the second term times the first term untouched. We can distribute the -e^x, add like terms together, and then factor the -e^x back out for simplicity’s sake.

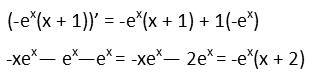
That was our first derivative. To find our second derivative, we derive the result of the first.

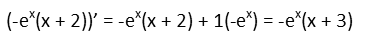
I think I see a pattern already, but let’s do it one more time to find the third derivative, just to make sure.

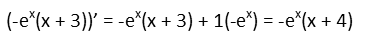
There definitely IS a pattern emerging. The -e^x is never going to change. It’s just going to stay the same. But the parenthetical term is seeing its constant increase by one every time we take a derivative. In fact, that constant is exactly one higher than the derivative. So, for our 100th derivative, it should be 101:

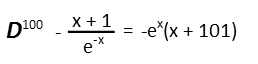
And there we found it. I was pretty confident of what was happening after the second derivative, but we did three just to confirm. By recognizing the pattern, we saved ourselves a LOT of work – 97 more derivatives worth of work!. Also note I used two different types of notation for the derivative here: Lagrane’s notation, which makes use of the prime ( ‘ ) symbol, and Euler’s notation, which uses just the capital italicized D with an exponent telling us how many derivatives to take. Lagrange’s notation is more compact for one or two derivatives, but it becomes really clunky after 3 – you have to add another prime symbol for every derivative, so 100 would have been highly unwieldy.