Math Made Easy: Problem of the Day 137

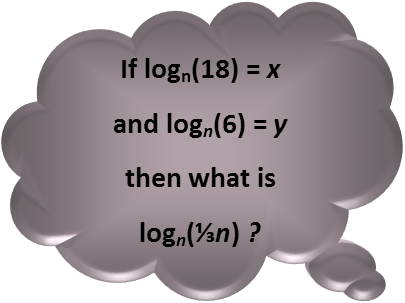
Those pesky, pesky logarithms. If they were original devised to make multiplication and exponentials easier, why do so many people dread them? Remember that they came about several hundred years ago, before the age of calculators. Working with many exponentials was an incredibly tedious task when you had to do everything by hand, on paper. But, even today, in the age of calculators, they are still a useful tool to help make our math easier in some places. As such, it’s a good idea to get used to manipulating them.

A common strategy when dealing with logarithms is to rewrite everything in exponential form. Don’t do that for today. While it can be a good strategy sometimes, it will make this problem much harder, as you’d get one n^x = 18 and n^y = 6. These are the very kinds of problems logarithms were invented to help solve. Instead of rewriting these logs as exponentials, let’s look into some way to take advantage of the rules of logarithms to rewrite them as different logarithms.

Immediately we should see we can rewrite the one we’re asked to evaluate. Let’s first recognize that we can combine the term inside the log as a single fraction. This makes it the division of two things, so we can use the quotient property of logarithms to separate it into two different logarithms – one with the top term minus another log with the bottom term.

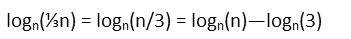
Seeing that, we look at our other logs. 18, 6, and 3 are all related – they’re all multiples of 3. In fact, we can actually get three if we divide 18 by 6. Wait, why don’t we rewrite log_n(3) as log_n(18/6)? If we do that, we can again take advantage of the quotient rule of exponents to rewrite log_n(3) as two different, and known, logarithms.

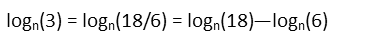
We plug those into our rewritten version of the log we’re trying to evaluate, being careful to place them in parentheses. We then distribute the minus sign so we can drop the parentheses. We recognize that the log of anything to its own base is 1, and we replace the log_n’s of 18 and 6 with their equivalencies, giving us our final, much simplified expression, sans all logarithms.

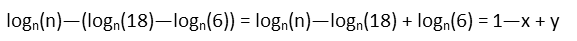
Now were we given a means to evaluate x and y, we could even simply solve the problem through subtraction and addition. And that’s exactly how logarithms were meant to work – take a difficult exponential expression and turn it into something we can solve almost solely with simple addition and subtraction. So don’t be too intimidated by them. They’ve been around for centuries for a reason.