Math Made Easy: Problem of the Day 138

For today, I thought it might be fun to revisit the lightsaber problem we did way back in Problem of the Day 27. In that problem, we made the ridiculous assumption that a single photon, oscillating back and forth along the length of 1 meter, could impart all of its energy to every atom upon its path. We contemplated how much energy that would be, and whether the beam thus created could cut through matter. Today, let’s be a bit more realistic about our approach to the question: Can lightsabers really work?

I picked iron for the material through which we’re going to try to cut today for simplicity’s sake. Each material will have a different amount of energy needed to cut through it. Iron’s pretty tough, and while steel is stronger, and has a higher melting temperature, it wouldn’t take too terribly much more energy to cut through steel than iron. So we’ll work with the simpler one (since iron is an element and steel, being an alloy, comes in many different varieties).

First, let’s consider how much energy it would take to vaporize a cylinder of iron. We pick a cylinder since lightsabers are assumed to be cylindrical in shape, so any path they cut through an object is itself going to be cylindrical. We’ll consider the saber to be cutting directly through, using the shortest path through the iron. So we’ll define the dimensions of the cylinder of the iron as the 10cm thickness and the 1cm radius of the lightsaber. This gives us the following volume for our iron:

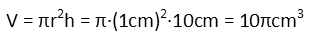
Now let’s figure out how many atoms are in the chunk of iron, and how much energy it will take to vaporize them. We know the density of iron, and its vaporization energy by mass from experiment:

Knowing the vaporization energy based on mass, and the density of iron, we can determine the vaporization energy per cubic centimeter:

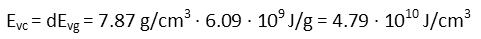
With that, we can multiply the volume of the cylinder to determine how much total energy will be needed to vaporize a path through our chunk of iron:

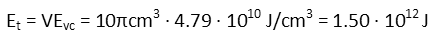
To give you an idea of how much energy that is, it’s about half the energy contained in the ENTIRE fuel capacity of an Airbus A330. That’s a LOT of energy. And here’s where things get problematic. If that energy weren’t needed to be delivered all at once, but over time, it might be more realistic. But when we watch the clips of lightsabers cutting through things, they do it almost instantaneously. Even in the clip where Qui-Gon is cutting through the blast doors on the trade federation ship, when he initially stabs them with the lightsaber, it does so instantaneously – the space occupied by the blade of the saber is instantaneously vaporized. So every 10cm length of the saber delivers at LEAST enough energy to do that. The blades look to be about one meter long on average, so that means those little handles are producing blades that put out 10 times that, so 1.50x10^13> Joules of energy every instant. The shortest instant is that of each individual photon. So let’s figure out how much energy each photon might need.

I’ll do that by assuming one photon to one atom. Sure, the energy could be delivered over multiple photons, assuming they are the appropriate wavelength for the atoms to even be able to absorb them. And here I’ll take a little sidetrack – that’s another problem. Lightsabers in the movies are continually referenced as being made solely of light. This makes them problematic as cutting tools. Photons cannot deliver just part of their energy to an atom. It’s an all or nothing prospect. And it’s worse than that – each photon has to be exactly the right wavelength. Each atom has only certain wavelengths of light it can absorb. If the photon is not one of those wavelengths, it doesn’t matter how much energy it has, it cannot and will not be absorbed by the atom. It’ll either bounce of or pass right by harmlessly. So blades made up of a single color of light, which would mean all the photons are one wavelength, would be effective against some materials, and not so much against others. Anyway, let’s calculate the average amount of energy per atom, and we’ll see what kind of photons would be needed to deliver that.

We know the molar mass of iron. That means how much one mole of iron atoms weigh. From that, we can get an average mass of iron atoms per gram. This is just a conversion so we can use the figures we’ve already calculated.

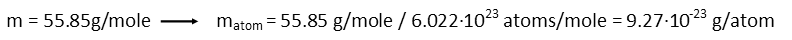
With the mass in grams per atom, and the density of iron, we can determine how many atoms are in one cubic centimeter of iron:

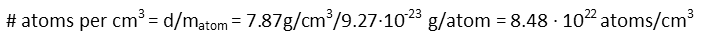
We multiply that by the volume of our cylinder to determine how many atoms are in it:

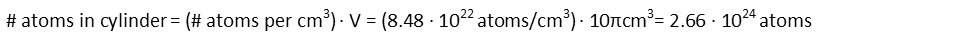
And now we divide the energy need to vaporize them by the number of iron atoms to find the average energy needed per atom:

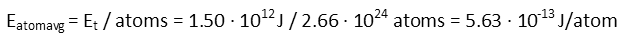
Back in Problem of the Day 27, we calculated that each photon of Luke’s blue lightsaber carried 1.255x10^-10 Joules of energy. That’s three orders of magnitude too small! It would require photons with a wavelength in the x-ray spectrum to carry the needed energy. That is following the assumption that all the energy needs to be delivered instantaneously, and therefor each atom is struck by only one photon. And that means the blades would not be visible.

Now, this would not be as problematic if the blades were made of high-energy plasmas contained by looped magnetic fields. Then we’re dealing with thermal properties of the blade and the quantum mechanics of light don’t actually introduce any the problems of photons being the wrong wavelength.

But, as I said in the last article, Star Wars is fantasy. It doesn’t have to follow the laws of physics, and we’re okay with that. Let’s just enjoy the story and the flashiness and the pew pew pew!