Math Made Easy: Problem of the Day 139

The “imaginary” number i is an interesting number. Defined as the square root of negative one, it’s called imaginary because, without it, there is no way to take the square root of any negative number. It doesn’t exist in a traditional Euclidean space. But it DOES exist, and have a very real effect, in our physical universe, which is why we have to learn how to deal with it in our mathematics. We see its effects in the way electricity behaves, ocean waves, light, and anything else that has the behavioural characteristics of wave phenomena.

In high school, you may be made to do various powers of i, and taught to recognize the oscillating pattern of its signs as its raised to various exponents, but rarely do you really have to do much with roots of it beyond having to simplify radicals with it inside. And with those, you’re normally told you’re done once you have an i you can’t pull out of the radical.

So what do you do when you’re asked for a root of i, and an answer without a radical is desired? Well, let’s first consider the cube root of it in the simplest way. If we multiply i times itself three times, or cube it, we’ll end up with -i. That’s because i² is in there, and that will flip the sign. So let’s conjecture that the cube root of i must be -i, and test it:

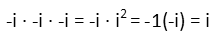
Well, there it is. BUT. That’s not the answer for which we were asked. We want the cube root in terms of sines and cosines. How do we get that?

To get there, let’s look at Euler’s Identity. It states that:

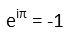
If we take the square root of both sides, we effectively have i on the right hand side, since it is the square root of negative one.

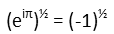
Now we take the cube root of that. I’m keeping everything in exponential notation instead of radicals to make the algebra easier. It allows us to use the product rule of exponents to simplify. That tells us we can just multiply the exponents.

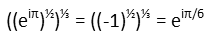
We ended up with something that looks like an angle measure in radians in the exponent of e. So let’s look at Euler’s Formula now (which is where Euler’s Identity comes from):

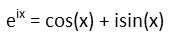
In our result, π/6 is the x in Euler’s Formula. That allows us to directly convert our result into sines and cosines. Which gives us the answer we wanted.

And this is an interesting result. Since we can express the cube root of i in terms of sines and cosines, we can recognize that there are actually an infinite number of angles that will give the same result, since the sine and cosines functions are infinitely repeating. That means there are actually an infinite number of cube roots of i. But we’ll just leave it at the one we found and be satisfied with our result – we really don’t need any of the larger angle results unless we were working with a system that called for them.