Math Made Easy: Problem of the Day 14
In Memorium: David Bowie
I received a request for today’s Problem of the Day, and I’m going to go ahead and honor it. Yesterday the music world suffered a great loss in the passing of David Bowie. People are waking up to this reality, and we’re all starting our mourning. In an effort to help comfort people, Simon Pegg made the following tweet:

So, for today’s problem, just what ARE the odds any given human would have been born while David Bowie was alive? Try to think about this on your own before you read on.
There are two things we need to consider when trying to figure this out.
First, how many people have ever existed. I’m going to use to figures – the current estimate is that a total of somewhere between 100 and 115 billion humans have lived in all of human history. Also, the United Nations estimated that there’ll be 11.2 billion people by the year 2100, and a bit over 7 billion are alive today. So, lets account for those extra people, and say that, deaths included, oh, 125 billion people will have existed by 2100. We’ll use that as for our low-end probability. On the high end, we’ll use the smaller figure of only 100 billion people having ever existed.
The second thing we need to consider, is how long have humans been on the Earth? Pegg’s tweet implies we need to consider the entire 4.5 billion years of Earth’s existence. I’ll argue that isn’t true, as humans have only been around for a short period of time. The odds of any human having existed before our species did are exactly zero. So we can ignore most of that 4.5 billion years and only account for the time we’ve existed. I’ll use the 200,000 years in which anatomically modern humans have existed.
So, we calculate first the odds that any given human is you. That is simply one divided by the total number of humans. Then we multiply that by the fraction of human existence that was David Bowie’s lifespan: 65/2x105. I have both the low and high end calculations below.
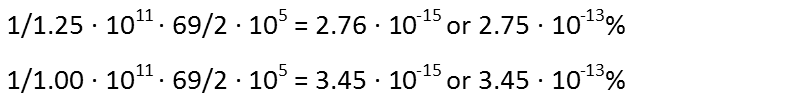
We see that the odds of you having existed at the same time as Bowie are still pretty slim, even acknowledging the constraint that you can only have been born sometimes in the existence of humanity. At best, you only had a 3.45x10-13 percent chance of being around in his lifetime. To put that in perspective, you have a whopping 3.42x10-7 percent chance of winning the current Powerball lottery, should you play. So you beat the odds just by being around to experience the joy of Bowie’s music.
Note: I used simple probability for this article for quick, off the cuff calculations to illustrate Simon Pegg’s point. Calculating the odds of you existing is actually far more complicated since human growth doesn’t happen at a consistent rate, and, just like Bowie, you occupy more than just a point in the timeline of human history.
Addendum: So there is another way to approach the problem, one that gives a very different probability. If one considers that, throughout the course of Bowie's lifetime, around 11 billion people have lived, we can consider each of those people as a "slot' which you could potentially fill. Now we can use combinatorial probability instead of simple probability to try to figure out the odds of you being alive when he was. First, we consider how many permutations of you there are in that 11 billion, using this formula, where n is the total number of available "slots" for you, and r is the total number possible yous (1):
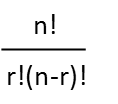
And we divide that by the total number possible outcomes of people, which would be the total number of people who have ever existed:
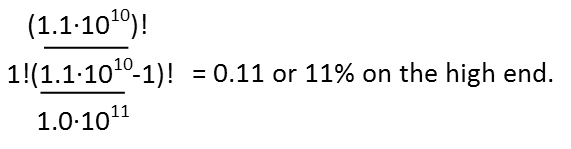
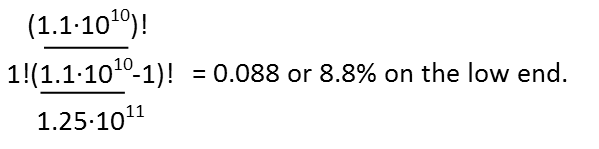
Which gives us a significantly higher chance of you having existed during his lifetime. A small one still, but not near as remote. Note that, effectively, because there's only one you, it does look like simple probability (and in fact, really is just 11 billion divided by 100 or 125 billion because of the fun way the factorials cancel), but without taking into account that you could have been born at any time. Honestly, I could see both arguments as having validity.
|



