Math Made Easy: Problem of the Day 141

I do a lot of exponent evaluate challenges. In my tutoring, I find that manipulating exponential terms is one of the areas at which most of my students struggle, so it seems that one can’t practice it enough. Most the techniques one can use to work with them seem obvious in hindsight, and should be in foresight, but they don’t always come to mind. So let’s tackle today’s and see how easy we can make it.

Common base. I can’t say it enough, we always want to look for a common base. This expression almost has that, but it has two coefficients – one for the subtracted term in the numerator and one for the term in the denominator. But we shouldn’t let that throw us. That term, too, has a common base. We just need to write it so we can see it. Any number can be written as itself raised to the first power. So let’s write it that way.

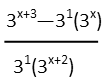
Doing this, we see the base of 3 more readily. We also see that in both those terms, we’re dealing with the product rule of exponents – one exponential multiplied by another, both with common bases. That tells us we can just add the exponents. So up top we add one to x, and down below we add it to x + 2, and we get the following:

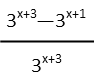
Now let’s break this up into two fractions. Since we only have one term in the denominator, this is easy enough to do – the first fraction’s numerator will have the first term up top, and from that we’ll subtract the second fraction (since the two numerator terms are separated by a minus) whose top is the second term in the original numerator. Like so:

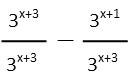
Having done that, we see the first fraction evaluates to 1 since its top and bottom are the same. We don’t have to worry about the domain since no value for x will produce zero. For the second fraction, we can apply the quotient rule of exponents, which tells us we can write it as a single exponential with exponent being the top minus the bottom. Since they’re both binomials, I’ll write it out to keep it clear. We distribute the minus sign, the x’s will cancel, and we can subtract the constants, giving us a single negative exponent. How convenient that the variables all went away. Remember that negative exponent means just the reciprocal of the same number with a positive exponent.

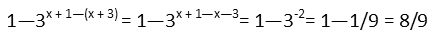
And our expression evaluates to a nice rational number, no variables. One might not have suspected that upon first glance at it. But just rewriting so everything had a common base, a little algebra, and following the rules of exponents led us to a nice, easy solution.