Math Made Easy: Problem of the Day 15

We’re going to mix exponents and factorials today. Here’s the problem at which we’re going to take a look. Simplify it.

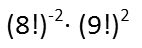
This problem is actually fairly simple. It just requires remembering what factorials and exponents mean, and how to take advantage of their properties to simplify the expression with very little computation involved. You don’t need a calculator, and you don’t need to actually compute the factorials. First, let’s recognize that a negative exponent (outside of trigonometric functions) just represent the reciprocal of a positive exponent. So (8!)^-2 is just 1/(8!)². We’ll rewrite our expression recognizing that, so now we have a fraction. I have an inkling it might help to break up the exponents into what they represent – in other words, a thing times itself however many times the exponent says, so I’ll write that out in my next step. Then, we recognize that a factorial is an operator telling you to multiply the number to the left by every positive integer between it and zero, ie, 4! = 4x3x2x1. This means that any factorial is part of the factorial of a higher positive integer. So 8! Is part of 9!. The only thing missing is 9. So we’ll rewrite our expression to recognize this, with 9! Broken out to 9x8!.

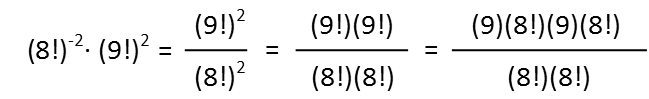
Now we can clearly see that I have two sets of 8! In both top and bottom. I can cancel all of those, leaving me with nothing in the denominator, and just 9x9 (or 9²) in the numerator. It’s the only actual computation I have to make, and it’s an easy one. We see our expression simplifies to the positive integer 81. And we’re done.

So when you see factorials and exponents, just remember how they work, and keep it simple. Frequently you’ll be able to make your problem easier than it appears to be, and reduce the amount of actual computation you have to do.