Math Made Easy: Problem of the Day 16

Our painter is back. This time he’s asked to paint the shape below on a wall. The top and bottom lines are formed by the ceiling. The wall is 8 meters high, the wall 6 meters wide, and he is assured the building is level, so the ceiling and floor are parallel, and square. The triangles are to be two colors, black and gold, alternating, and the centerline is to bisect the wall. If one bucket of paint covers 1m² of wall, how many buckets does he need to buy of each color?

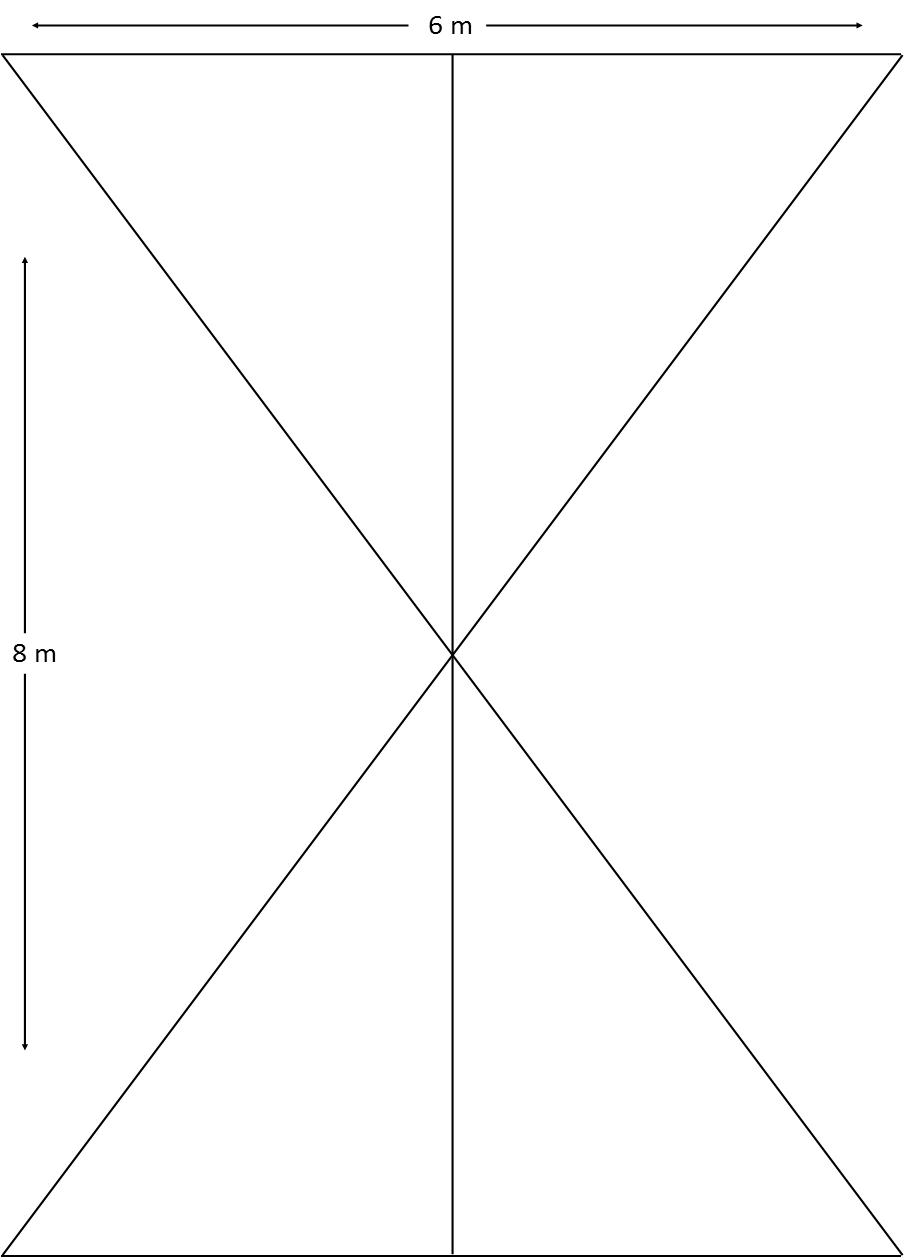
First, we need to consider the geometry of the situation. If the centerline is a bisector, then, segment bisector definition, the base of each triangle is congruent, or the same length. Each triangle on the floor shares a leg, as do the ones on the ceiling. By reflexive property (a thing is itself), this means each of those triangles has a leg of the same side. And by the theorem of alternate interior angles of parallel lines, we know that both angles formed by each transversal are congruent. And since the angles that bisector forms with the floor and ceiling are right angles (since the building is square), we now know that all 4 triangles are congruent: the Side Angle Side theorem tells us that each triangle on the floor is the same dimension, as well as each on the ceiling, and corresponding angles tells us that the top triangles are congruent to the bottom triangles.

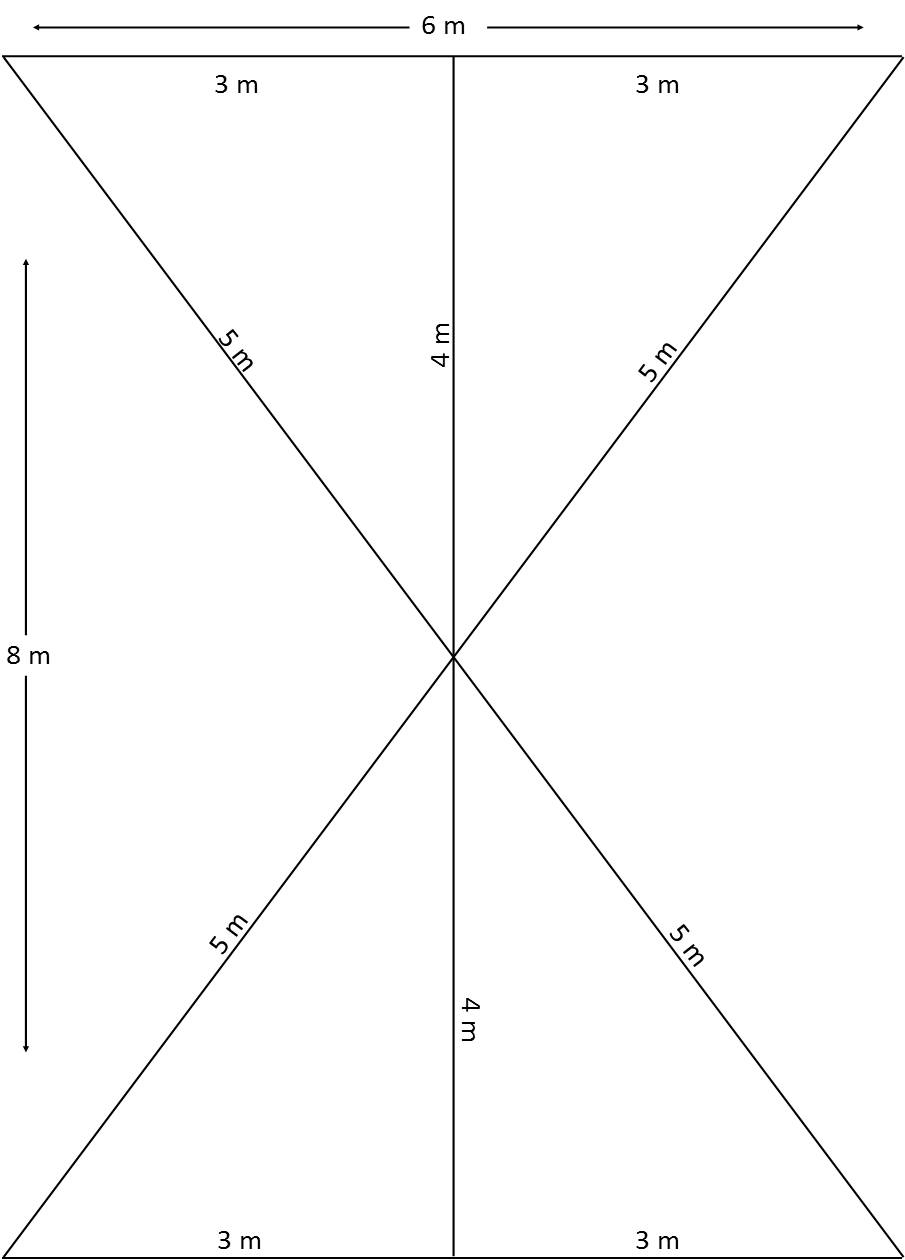
This congruency is convenient – it means that we only have to make a couple calculations to figure out how much paint we need. We know the bases are all 3 meters, since they’re each half the width of the wall, and the legs are 4 meters, since they’re half the height of the ceiling. We could use the Pythagorean Theorem to calculate the length of the hypotenuses (and I did, just for the heck of it -perhaps he’d like to use a different paint to make an outline of the design), but we don’t actually need it to accomplish what the painter needs.

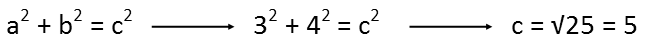
All we need is the formula for the area of a triangle. The general form of it that applies to all triangles is the first form we see below. a and b are two adjacent sides, and θ is the included angle. Here the included angle is π/2 (or 90 degrees), and the sine of that is just 1, so it drops out. That’s why the formula for the area of a right triangle is ½bh – it’s a special case of the general formula, where the sine of a right angle is 1, and the two adjacent sides are the base and the height of the triangle.

So, given that, we find the area of each triangle is 6m², which means he needs 6 buckets of paint for each triangle. Since they’re alternating, and he’s using two colours, that means he need to paint two triangles gold and two black, so he needs 12 buckets of black paint and 12 of gold.