Math Made Easy: Problem of the Day 17
We havenít really played with trigonometric identities much yet, so letís do that today. The key to solving most problems with trigonometric functions in them, is understanding your trigonometric identities, as well as the relationships between the various functions. Something that may look difficult may prove not to be so if you can find ways to manipulate the expression to look more like something youíre familiar with, especially an identity.
Consider todayís problem. Try to evaluate this expression with no calculator. Remember you can always use the unit circle Ė if you donít have one, a google search will find you plenty of them.
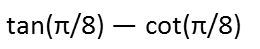
We see that π/8 is not on our unit circle. So how can we evaluate this without a calculator? Letís see if we can produce any identities. The first thing Iím going to do, is Iím going to rewrite tangent and cotangent in terms of sine and cosine. After doing that, I want to make this one fraction, so Iím going to give them a common denominator by multiplying the first one by sine over sine and the second by cosine over cosine, giving me the expression at the end here. Note that Iím not writing (θ) for a lot of my work as, when an angle is not specified in trigonometric functions, itís assumed to be the same angle for all functions involved. Iíll put it back in later when itís necessary.
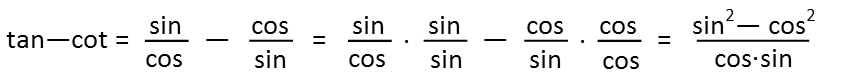
I think Iím starting to see something more familiar. Look at the top, it ALMOST looks like a double angle for cosine, but not quite. What if I get sneaky and multiply the whole thing by -1? Then the signs reverse, and I actually DO have a double angle for cosine up top. Now letís look at the bottom. It is almost the double angle for sine, but not quite. Iím going to be even sneakier now. By multiplying the bottom by ½ AND 2 at the same time, Iím not changing it at all because they cancel, BUT I can now SEE a double angle for sine. And so I replace it with such. And now that Iíve replaced top and bottom with double angles, I pull that ½ out of the bottom, it becomes a big 2, and I can rewrite the whole thing as just -2cot(θ).
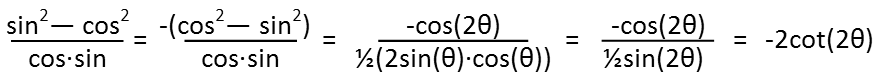
So now that I have that, I can plug my π/8 back in. Multiplied by 2, thatís just π/4, and that IS on the unit circle. The cot is the cosine over the sine, as we already showed, and those are both √2/2 at π/4 radians. That evaluates to 1, so our original expression evaluates to -2. Weíre done. No calculator needed whatsoever.
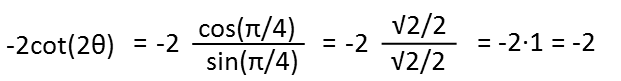
Todayís problem was all about remembering your trig idents, and being clever with little ways to multiply things by one that doesnít actually change the value of your expression, but changes its appearance so you can better recognize what it is, and more easily manipulate it.
|



