Math Made Easy: Problem of the Day 18

Here’s a real world math problem with which we all have to deal. In the United States, Sales tax is not displayed on the price tag. The customer is expected to be able to calculate it. And sometimes, when a sale is going on, the price tag is also not modified – again, the customer is expected to figure it out. What does this mean? We need math! So let’s look at a situation you might encounter. An item is marked down at 20% off. The store is having a one-day half off everything sale, and they allow sales to stack (unlike many stores that actually only allow one discount to apply). In the store’s city, sales tax is 5%. If the item was originally $10, how much does the customer owe at the counter? Can you calculate this without using a calculator? It’s possible, and you don’t always have one in the store.

The easiest way to do this problem is in fractions. But we need to consider what fractions we’re going to use. The first thing we need to recognize is that all those discounts are percentages less than 100%. That means that something that is 20% of is worth 80% of the original. And to determine that price, we just multiply that 80% times the original price. And this works as a nice little chain, so if there’s another discount on that, we multiply by it (50% for the next one, since half off is 50%). For tax, that’s in addition to 100%, so 5% tax means multiply by 105%. And percentages are just that number over 100 when represented as a fraction, so our whole expression looks like this (Note that I’ve put the dollar value over one to be consistent and have everything represented as a fraction):

Now that we have them all lined up as fractions, we’re going to take advantage of that form to make our calculations easier. We’re going to simplify BEFORE we multiply, and we’re going to do it in faster, easier steps rather than trying to find a greatest common factor like most of were taught to do in elementary school. But before we do that, we need to take care of that pesky decimal. It’s easy enough – whenever you see a decimal in the fraction, or more than one, just move the decimal point to the right until it’s no longer there. And at the same time, do move the decimal of the other side of the fraction the same number of places, adding zeroes as necessary – the key is you have to move the decimal in BOTH the numerator and denominator the same number of places. Here, it’s two places in the numerator, there’s no decimal in the denominator, so we add two zeroes so we can do so. After we do that, we can start simplifying.

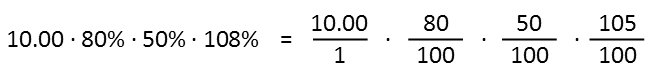
For my first simplification, I’m going to find matching zeroes in numerators and denominators, and eliminate them one-for-one (the same number of zeroes in both numerator and denominator). Note I could have just dropped the zeroes after the decimal in the fraction representing our original money, but I left them in there for illustrative purposes.

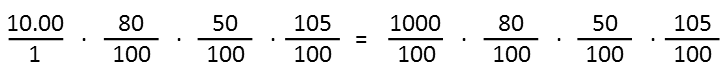
I see a ten in one of the numerators, and one in two of the denominators. I’m going to cancel the one in the numerator and one of the ones in the denominators. Next, I’m going to find even numbers, paired in numerators and denominators (one-for-one), and factor a 2 out of them. I can pick from any numerator, and any denominator in this chain of multiplication, so long as I’m doing it in pairs – one numerator for one denominator. I’m going to repeat that until I can’t pull any more twos out in pairs.

Now I see a pair of 5’s. I’ll cancel them right off. I also see that in the last fraction, I have factors of 5 in the numerator and denominator, so I’ll reduce them accordingly.

I’ve reduced the whole thing to a single fraction, 21/5, and it doesn’t look like I can go any further. But that’s great, because I haven’t had to multiply a single thing, and this is going to be much easier to divide. Now here’s my trick for easily dividing things in my head, with no calculator, no paper. I break them up. I recognize that:

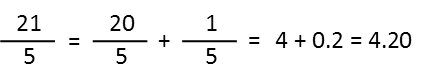
Now they’re easy to do! 20/5 simplifies to 4/1, which is just 4. And 1/5 is the same thing as 10/5 with the decimal moved to the left once, which is 0.2. I put them back together, and our price at the register is $4.20.

Now, a lot of people would have figure out what the first discount is, then applied the second to that, then the sales tax to that result. Which is a viable way to do it, and for this problem, wouldn’t have actually been that hard. But I did make the numbers a little easier on this problem on purpose. The technique I used end up being easier in all situations, when those percentages don’t work out quite as nicely as they did in mine (like, say, oh, a 75% off situation and maybe a 8.5% sales tax). BUT. Use what works for you – many math problems have lots of ways to do them, and the smart person uses the tool that works best for the situation.